Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Xét ΔAEH và ΔADC có:
∠(AEH) = ∠(ADC) = 90 0
∠(DAC) là góc chung
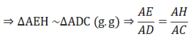
⇒ AE.AC = AD.AH
Xét Δ BEC và ΔADC có:
∠(BEC) = ∠(ADC) = 90 0
∠(ACD) là góc chung
⇒ ΔBEC ∼ ΔADC (g.g)
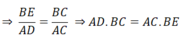

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
DO đó: ΔABE\(\sim\)ΔACF
SUy ra: AB/AC=AE/AF
hay \(AB\cdot AF=AE\cdot AC\)
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc EAF chung
Do đó: ΔAEF\(\sim\)ΔABC
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)

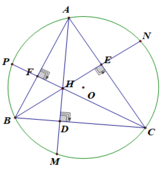
Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [B, C] Đoạn thẳng l: Đoạn thẳng [P, C] Đoạn thẳng m: Đoạn thẳng [M, A] Đoạn thẳng n: Đoạn thẳng [B, N] O = (1.97, 2.92) O = (1.97, 2.92) O = (1.97, 2.92) Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm A: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm B: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm C: Điểm trên c Điểm P: Giao điểm của c, j Điểm P: Giao điểm của c, j Điểm P: Giao điểm của c, j Điểm M: Giao điểm của c, k Điểm M: Giao điểm của c, k Điểm M: Giao điểm của c, k Điểm N: Giao điểm của c, i Điểm N: Giao điểm của c, i Điểm N: Giao điểm của c, i Điểm F: Giao điểm của j, f Điểm F: Giao điểm của j, f Điểm F: Giao điểm của j, f Điểm E: Giao điểm của i, g Điểm E: Giao điểm của i, g Điểm E: Giao điểm của i, g Điểm D: Giao điểm của k, h Điểm D: Giao điểm của k, h Điểm D: Giao điểm của k, h Điểm H: Giao điểm của l, m Điểm H: Giao điểm của l, m Điểm H: Giao điểm của l, m
a. Tứ giác CEHD có \(\widehat{HEC}=\widehat{HDC}=90^o\Rightarrow\) nó là tứ giác nội tiếp.
b. Tứ giác BFEC có \(\widehat{BEC}=\widehat{BFC}=90^o\Rightarrow\)nó là tứ giác nội tiếp. Vậy 4 điểm B, C, E, F cùng thuộc một đường tròn.
c. Ta thấy \(\Delta HAE\sim\Delta CAD\left(g-g\right)\Rightarrow\frac{AH}{AC}=\frac{AE}{AD}\Rightarrow AE.AC=AH.AD\)
Ta thấy \(\Delta CBE\sim\Delta CAD\left(g-g\right)\Rightarrow\frac{BC}{AC}=\frac{BE}{AD}\Rightarrow AD.BC=BE.AC\)
d. Ta thấy ngay \(\widehat{PCB}=\widehat{BAM}\) (Cùng phụ với góc ABC)
Mà \(\widehat{BAM}=\widehat{BCM}\) (Góc nội tiếp cùng chắn cung BM)
Vậy nên \(\widehat{PCB}=\widehat{BCM}\) hay CM là phân giác góc \(\widehat{PCB}\)
Lại có \(CM⊥HD\) nên HCM là tam giác cân. Vậy CB là trung trực của HM hay H, M đối xứng nhau qua BC.
e. Ta thấy BFHD là tứ giác nội tiếp nên \(\widehat{FDH}=\widehat{FBH}\) (Góc nội tiếp cùng chẵn cung FH)
DHEC cùng là tứ giác nội tiếp nên \(\widehat{HDE}=\widehat{HCE}\) (Góc nội tiếp cùng chẵn cung HE)
Mà \(\widehat{FBH}=\widehat{HCE}\) ( Cùng phụ với góc \(\widehat{BAC}\) )
nên \(\widehat{FDH}=\widehat{HDE}\) hay DH là phân giác góc FDE.
Tương tự FH, EH cũng là phân giác góc DFE và DEF.
Vậy tâm đường tròn nội tiếp tam giác DEF chính là H.

a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
b: Xét ΔAHE vuông tại E và ΔACD vuông tại D có
\(\widehat{HAE}\) chung
Do đó: ΔAHE đồng dạng với ΔACD
=>\(\dfrac{AH}{AC}=\dfrac{AE}{AD}\)
=>\(AH\cdot AD=AC\cdot AE\)
Xét ΔABC có AD là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AD\cdot BC\left(1\right)\)
Xét ΔABC có BE là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot BE\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{1}{2}\cdot AD\cdot BC=\dfrac{1}{2}\cdot BE\cdot AC\)
=>\(AD\cdot BC=BE\cdot AC\)

a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: AH vuông góc với BC tại D
b: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
Do đó: ΔAEH đồnbg dạng với ΔADC
Suy ra: AE/AD=AH/AC
hay \(AE\cdot AC=AH\cdot AD\)

1. Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.
~ Ủng hộ nha ~
1. Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.
~ Ủng hộ nha ~

Câu hỏi của hungbck5 - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.