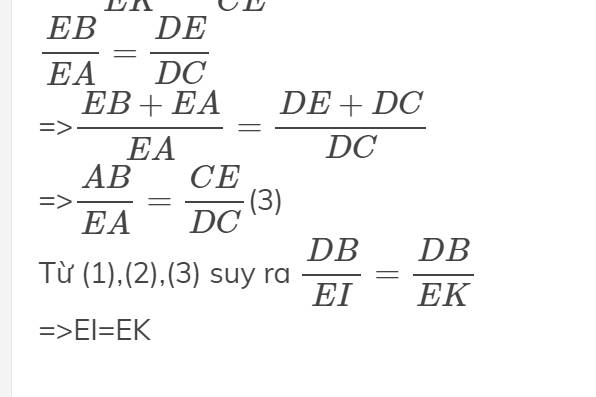Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự vẽ hình nha
c) ta có \(\widehat{EFA\:}+\widehat{EAF}=90^0;\widehat{EAK}+\widehat{EAF}=90^0\Rightarrow\widehat{EFA}=\widehat{EAK}\left(1\right)\)
vì BC // EF ⇒ AE ⊥ EF
\(\widehat{BEF}+\widehat{AEB}=90^0;\widehat{AEB}+\widehat{KEA}=90^0\Rightarrow\widehat{BEF}=\widehat{KEA\left(2\right)}\)
xét △KEA và △EBF có
(1) và (2)
⇒ △KEA ~ △BEF(g - g)
⇒ \(\frac{KE}{BE}=\frac{AE}{EF}\Rightarrow\frac{KE}{AE}=\frac{BE}{EF}\left(3\right)\)
xét △KEB và △AEF có
(3); \(\widehat{BEK}=\widehat{AEF}=90^0\)
⇒ △KEB ~ △AEF (g - g)
⇒ \(\frac{EB}{EF}=\frac{BK}{AF}\) ⇒ BE.AF = BK.EF ⇒ đpcm

a: Ta có: DB\(\perp\)AB
AC\(\perp\)AB
Do đó: DB//AC
Xét ΔECA có DB//AC
nên \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b: Xét ΔCEK có DB//EK
nên \(\dfrac{DB}{EK}=\dfrac{CD}{CE}\)(1)
Xét ΔAEI có DB//EI
nên \(\dfrac{DB}{EI}=\dfrac{AB}{AE}\left(2\right)\)
Ta có: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
=>\(\dfrac{BE+BA}{BA}=\dfrac{DE+DC}{DC}\)
=>\(\dfrac{AE}{BA}=\dfrac{CE}{DC}\)
=>\(\dfrac{CD}{CE}=\dfrac{AB}{AE}\left(3\right)\)
Từ (1),(2),(3) suy ra EI=EK