Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì B A C ^ = 90 o nên BC = 5. Khi đó
S 1 S 2 = π . 4 . 5 π . 3 . 5 = 4 3
Đáp án A

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
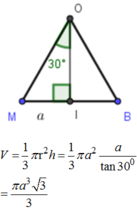
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

Đáp án B
Hình nón có chiều cao AB và bán kính BC. Diện tích xung quanh của hình nón là S = π a .2 a = 2 π a 2

Đáp án C.
Ta có A M = A B 2 − B C 2 2 = 2 a . Khi quay tam giác quanh trục MA thì ta được hình nón có bán kính r = a , đường cao h = 2 a . Thể tích khối nón là V = 1 3 π r 2 h = 2 3 π a 3 .

Chọn đáp án D
Phương pháp
Sử dụng công thức tính thể tích khối nón có bán kính đáy r và đương cao h là
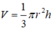
Cách giải
Quay tam giác ABC quanh đường thẳng AB ta được khối nón có bán kính đáy r=AC=b và đường cao h=AB=c. Khi đó thể tích của khối nón bằng
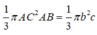

Đáp án A
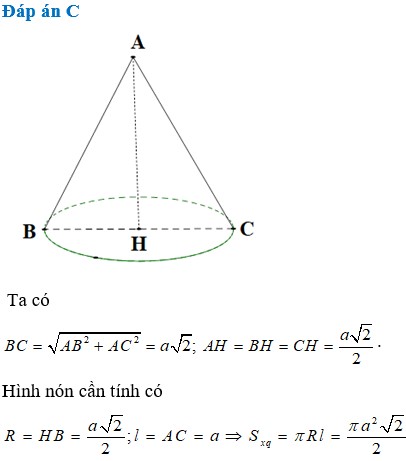
Chiều cao khối nón là A H = a 2 2 . Bán kính đáy là R = a 2 2
Thể tích khối nón là V = 1 3 π R 2 h = 1 3 π a 2 2 2 . a 2 2 = a 3 2 π 12