Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
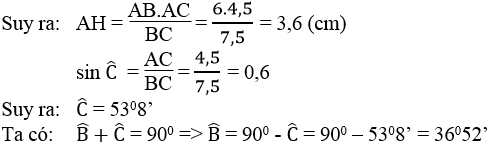b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
1 ,áp dụng bộ 3 pitago trong tam giác abc suy ra AC=5 cm dựa vào pitago đảo có : \(5^2+12^2\)= 13 suy ra tam giác ACD vuông tại c
S tứ giác = SABC +SADC =1/2 .3.4 +1/2. 5.12=36 cm ^2.
2,bài 2 vẽ hình lâu lém tự làm nha bn
3,
B1 minh da lam dc trc do roi nhung van cam on ban vi da giup do
A B C D 1 2 6v5
( v là căn nha bạn ; Ví dụ 8v5 là 8căn5 nha )
Ta có : \(SinABC=\frac{AC}{BC}\)
Mà : gócABC = 2.gócB2 ( BD là đường phân giác )
Do đó : \(SinABC=2.SinB_2\)
\(\Rightarrow sinB_2=\frac{1}{2}SinABC=\frac{1}{2}.\frac{AC}{BC}=\frac{AC}{2BC}\)
Ta có : \(SinB_1=\frac{AD}{BD}\)
Mà : góc B1 = góc B2 ( BD là đường phân giác )
\(\Rightarrow\frac{AD}{BD}=\frac{AC}{2BC}\)
\(\Rightarrow2BC=\frac{AC.BD}{AD}\)
\(\Rightarrow BC=\frac{AC.BD}{2.AD}=\frac{\left(AD+DC\right).6v5}{2.AD}\) ( 1 )
Ta có : 5AD = 3DC ( gt )
\(\Rightarrow AD=\frac{3DC}{5}=\frac{3}{5}DC\)
Thay : \(AD=\frac{3}{5}DC\) vào ( 1 ) Ta được :
\(BC=\frac{6v5.\left(\frac{3}{5}DC+DC\right)}{2.\left(\frac{3}{5}DC\right)}\)
\(BC=\frac{6v5.\left(\frac{8}{5}DC\right)}{\frac{6}{5}DC}\)
\(BC=\frac{\frac{48v5}{5}DC}{\frac{6}{5}DC}\)
\(BC=\frac{48v5}{6}\)
\(BC=8v5\)
Vậy BC = 8v5 cm
Học tốt !!!
Ta có:\(sin\widehat{BAH}\)=\(\frac{2}{3}\)\(\Rightarrow sin\widehat{BAH}\)\(\approx sin42^o\)
\(\Rightarrow\widehat{BAH}\)=\(42^o\)
Vì AH là đường cao => \(AH\perp BC=\left\{H\right\}\)
\(\Rightarrow\widehat{AHB}\)=\(\widehat{AHC}\)=\(90^O\)
Xét tam giác AHB vuông tại H:
\(\widehat{BAH}\)+\(\widehat{B}\)=\(90^O\)\(\Rightarrow\widehat{B}\)=\(48^O\)
Xét tam giác ABC vuông tại A, đường cao AH:
+) \(sin\widehat{B}\)=\(\frac{AC}{BC}\)\(\Leftrightarrow sin48^o=\frac{3}{BC}\)
\(\Rightarrow BC=4\left(cm\right)\)
+) \(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}\)
\(\Rightarrow AB\approx2,6\left(cm\right)\)
+) \(AH.BC=AB.AC\)(hệ thức giữa cạnh và đường cao)
\(\Rightarrow AH=\frac{AB.AC}{BC}\)
\(\Rightarrow AH\approx2\left(cm\right)\)
\(S\)ABC =\(\frac{AH.BC}{2}\)= \(4\left(cm^2\right)\)
*Mình sợ sẽ có sai sót nên bạn kiểm tra lại nhé
~HỌC TỐT~
Câu hỏi của Nguyễn Tấn Phát - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo!
A B C H
\(S_{\Delta ABC}=\frac{AH\cdot BC}{2}=\frac{6\cdot10}{2}=\frac{60}{2}=30\left(cm^2\right)\)
Vậy \(S_{\Delta ABC}=30cm^2\)
Cảm ơn bạn đã trả lời câu hỏi. Nhưng bạn trả lời sai rồi