Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

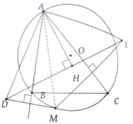
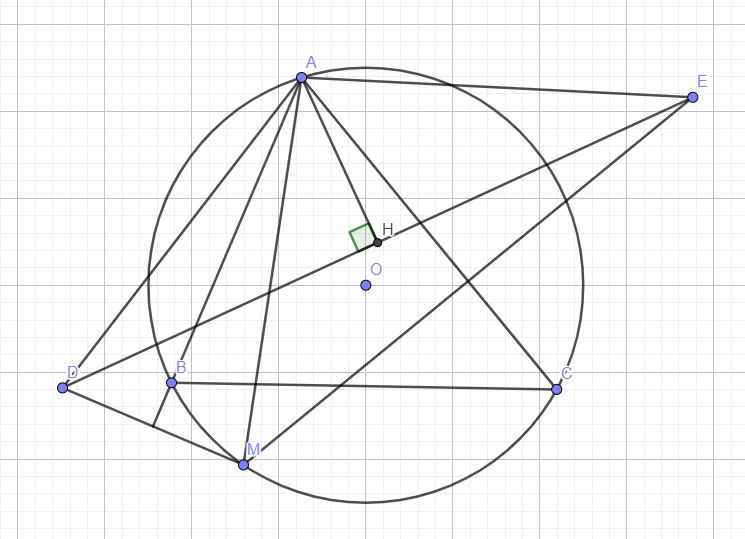
Kẻ AH ⊥ DE tại H
D A E ^ = 2 B A C ^
=> D A H ^ = B A C ^
Từ DE=2DH; AD=AM=AE
Suy ra DH=AD.sin D A H ^
Từ đó D E m a x <=> AM = 2R

Do D đối xứng M qua AB \(\Rightarrow\) AB là trung trực DM
\(\Rightarrow AM=AD\) và \(\widehat{DAB}=\widehat{MAB}\)
Tương tự ta có \(AM=AE\) và \(\widehat{CAM}=\widehat{CAE}\)
\(\Rightarrow\widehat{DAE}=\widehat{DAB}+\widehat{MAB}+\widehat{CAM}+\widehat{CAE}=2\left(\widehat{MAB}+\widehat{CAM}\right)=2\widehat{BAC}\)
Do \(AM=AD=AE\Rightarrow\Delta ADE\) cân tại A
Kẻ đường cao AH ứng với DE \(\Rightarrow\) H đồng thời là trung điểm DE và \(\widehat{DAH}=\dfrac{1}{2}\widehat{DAE}=\dfrac{1}{2}.2\widehat{BAC}=\widehat{BAC}\)
Trong tam giác vuông ADH:
\(sin\widehat{DAH}=\dfrac{DH}{AD}\Rightarrow DH=AD.sin\widehat{DAH}=AM.sin\widehat{BAC}\)
\(\Rightarrow\dfrac{1}{2}DE=AM.sin\widehat{BAC}\Rightarrow DE=2AM.sin\widehat{BAC}\)
Mà ABC cố định \(\Rightarrow DE_{max}\) khi \(AM_{max}\Rightarrow AM\) là đường kính của đường tròn
Hay M đối xứng A qua tâm O

a) Giả sử đã tìm được điểm D trên cung BC sao cho tứ giác BHCD là hình bình hành. Khi đó: BD//HC; CD//HB vì H là trực tâm tam giác ABC nên CH và BH
BD và CD.
Do đó: ABD = 900 và ACD = 900 .
Vậy AD là đường kính của đường tròn tâm O
Ngược lại nếu D là đầu đường kính AD của đường tròn tâm O thì tứ giác BHCD là hình bình hành.
b) Vì P đối xứng với D qua AB nên APB = ADB
nhưng ADB =ACB , ADB = ACB. Do đó: APB = ACB
Mặt khác: AHB + ACB = 1800 APB + AHB = 1800
Tứ giác APBH nội tiếp được đường tròn nên PAB = PHB
Mà PAB = DAB do đó: PHB = DAB
Chứng minh tương tự ta có: CHQ = DAC
Vậy PHQ = PHB + BHC + CHQ = BAC + BHC = 1800
Ba điểm P; H; Q thẳng hàng.
c) Ta thấy APQ là tam giác cân đỉnh A
Có AP = AQ = AD và PAQ = 2BAC không đổi nên cạnh đáy PQ đạt