Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
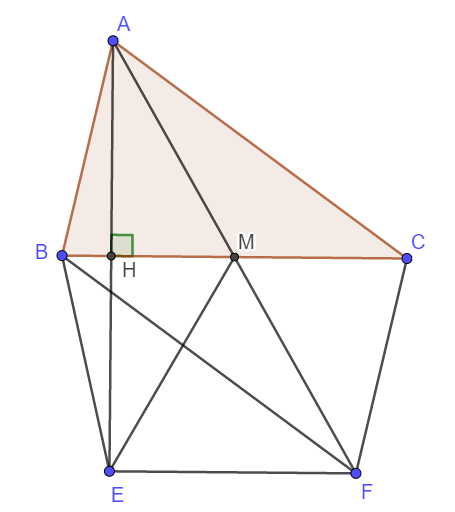
a) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên nó là tam giác cân.
Vậy thì MA = ME. Lại có MA = MF nên ME = MF.
b) Do AME là tam giác cân, MH là đường cao nên MH cũng là phân giác.
Vậy thì \(\widehat{AMB}=\widehat{BME}\)
Mà \(\widehat{AMB}=\widehat{CMF}\Rightarrow\widehat{BME}=\widehat{CMF}\)
Xét tam giác BME và CMF có:
BM = CM
ME = MF
\(\widehat{BME}=\widehat{CMF}\)
\(\Rightarrow\Delta BME=\Delta CMF\left(c-g-c\right)\)
\(\Rightarrow BE=CF\)
c) Dễ thấy \(\Delta BMF=\Delta CMA\left(c-g-c\right)\Rightarrow\widehat{BFM}=\widehat{CAM}\)
Chúng lại ở vị trí so le trong nên AC//BF.
d) Xét tam giác AEF có MA = ME = MF nên AEF là tam giác vuông. Vậy \(AE\perp EF\)
Lại có \(AE\perp BC\Rightarrow\) BC//EF
M A B C N H F D
a) Xét \(\Delta\)AHB và \(\Delta\)DHB có:
^AHB = ^DHB ( 1v )
HA = HD ( giả thiết )
MH chung
=> \(\Delta\)AHB = \(\Delta\)DHB ( c.g.c)
b) Từ (a) => ^ABH = ^DHB => BH là phân giác ^ABD
Vì \(\Delta\)ABC nhọn => H nằm trong đoạn BC
=> BC là phân giác ^ABD
c) NF vuông BC
AH vuông BC
=> NF // AH
=> ^NFM = ^HAM ( So le trong )
Lại có: ^HMA = NMF ( đối đỉnh ) và MA = MF ( giả thiết )
=> \(\Delta\)NFM = \(\Delta\)HAM ( g.c.g)
=> NF = AH ( 2)
Từ ( a) => AH = HD ( 3)
Từ (2) ; (3) => NF = HD
a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)
a) Xét ΔMAB và ΔMEC có
MA=ME(gt)
ˆAMB=ˆEMCAMB^=EMC^(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔMAB=ΔMEC(c-g-c)