Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác AMDN, ta có:
^A = ^N = ^M = 90o (gt)
Vậy tứ giác AMDN là hình chữ nhật.
b) *Xét △ABD, ta có:
K là trung điểm BD (gt)
I là trung điểm AD (gt)
⇒ KI là đường trung bình của △ABD.
⇒ KI // AB và KI = 12
AB. (1)
*Ta có:
DN ⊥ AC (gt)
AB ⊥ AC (△ABC vuông tại A)
⇒ DN // AB. (2)
Từ (1) và (2) suy ra KI // DN
*Xét △v ABC, ta có:
BD = CD (gt)
⇒ AD là đường trung tuyến
⇒ AD = BD = 12
AC
⇒ △ABD cân tại D
Mà DM ⊥ AB
⇒ DM là đường cao đồng thời là đường trung tuyến
⇒ MA = MB
*Ta có:
MA = 12
AB (cmt)
KI = 12
AB (cmt)
⇒MA = KI
Mà MA = DN (AMDN là hình chữ nhật)
Nên KI = DN
*Ta có:
KI // DN (cmt)
KI = DN (cmt)
Vậy INDK là hình bình hành
c) *Ta có:
KI //AM (KI // AB)
DM ⊥ AM (gt)
⇒KI ⊥ DM
*Xét tứ giác DIMK, ta có:
KI ⊥ DM (cmt)
Vậy DIMK là hình thoi.
d) Xét hình chữ nhật AMDN, ta có:
MN, AD là hai đường chéo
Mà I là trung điểm AD (gt)
Nên I là trung điểm MN
Vậy M, N đối xứng với nhau qua I.

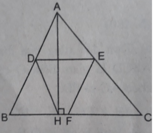
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2

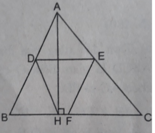
DECH là hình thang (vì có DE // CH);
BDEF là hình bình hành (vì có DE // BF và DE = BF)
DEFH là hình thang cân (vì có DE // HF và DF = HE = 1/2AC)

Bài 1:
a: Xét ΔABC có AE/AB=AN/AC
nên EN//BC
=>EN//HM
Xét tứ giác AEMN có
NM//AE
NM=AE
Do đó: AEMN là hình bình hành
mà góc NAE=90 độ
nên AEMN là hình chữ nhật
=>AM=NE
Ta có: ΔHCA vuông tại H
mà HN là trung tuyến
nên HN=AN=CN=ME
Ta có: ΔHAB vuông tại H
mà HE là trung tuyến
nên HE=AE=BE
Xét tứ giác MHEN có
MH//EN
ME=HN
Do đó: MHEN là hình bình hành
b: Xét ΔNAE và ΔNHE có
NA=NH
AE=HE
NE chung
Do đó: ΔNAE=ΔNHE
=>góc NHE=90 độ
c: Xét ΔEAK vuông tại E và ΔEBM vuông tạiE có
EA=EB
góc EAK=góc EBM
Do đó: ΔEAK=ΔEBM
=>EK=EM
Xét tứ giác AKBM có
E là trung điểm chung của AB và KM
MA=MB
Do đó; AKBM là hìnhthoi

Bạn tự vẽ hình nhé!
a) Xét tam giác ADC và tam giác BEC có:
\(\widehat{C}\)chung
\(\frac{CD}{CE}=\frac{CA}{CB}\)(2 tam giác vuông CDE và CAB đồng dạng)
=> Tam giác ADC đồng dạng với tam giác BEC (cgc) (đpcm)
b) Tam giác AHD vuông tại H (gt)
=> \(\widehat{BEC}=\widehat{ADC}=135^o\)
Nên \(\widehat{AEB}=45^o\)do đó tam giác ABE vuông tại A
=> BE=\(AB\sqrt{2}=3\sqrt{2}\)
Nguồn: Đặng Thị Nhiên
c) Tam giác ABE vuông tại A nên tia AM là phân giác BAC
\(\Rightarrow\frac{GB}{GC}=\frac{AB}{AC}\)
Vì tam giác ABC đồng dạng tam giác DEC nên:
\(\frac{AB}{AC}=\frac{ED}{DC}=\frac{AH}{HC}=\frac{HD}{HC}\)(DE//AH)
Do đó: \(\frac{GB}{GC}=\frac{HD}{HC}\Rightarrow\frac{GB}{GB+GC}=\frac{HD}{HD+HC}\Rightarrow\frac{GB}{GC}=\frac{AH}{AH+HC}\left(đpcm\right)\)
Nguồn: Đặng Thị Nhiên

Em tham khảo tại đây nhé.
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath
Câu hỏi của Trần Nam Anh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
A C 2 = A H 2 + H C 2 = 8 2 + 6 2 = 10 2 ⇒ AC = 10cm;
HE = 1/2 AC = 1/2.10 = 5 (cm).