Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
góc AHC=90 độ
=>AHCE là hình chữ nhật
b: Xét ΔAHC có
HI,AM là trung tuyến
HI cắt AM tại G
=>G là trọng tâm
=>HG=2/3HI=2/3*1/2*HE=1/3HE
Xét ΔCAE có
AN,EI là trung tuyến
AN cắt EI tại K
=>K là trọng tâm
=>EK=2/3EI=1/3EH
HG+GK+KE=HE
=>GK=HE-1/3HE-1/3HE=1/3HE
=>HG=GK=KE

a: Xét tứ giác AHCE có
I là trung điểm chung của AC,HE
góc AHC=90 độ
HA=HC
=>AHCE là hình vuông
b: Để AHCE là hình vuông thì ΔABC cần có những điều kiện sau:
AB=AC; góc B=45 độ

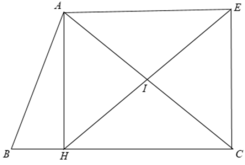
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.

a: Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật

a) Xét tứ giác AHCE có:
+ D là trung điểm của AC (gt).
+ D là trung điểm của HE (do E đối xứng với H qua D).
=> Tứ giác AHCE là hình bình hành (dhnb).
Mà ^AHC = 90o (AH vuông góc BC).
=> Tứ giác AHCE là hình chữ nhật (dhnb).
Xét tứ giác AHBN có:
+ M là trung điểm của AB (gt).
+ M là trung điểm của HN (do N đối xứng với H qua M).
=> Tứ giác AHBN là hình bình hành (dhnb).
Mà ^AHB = 90o (AH vuông góc BC).
=> Tứ giác AHBN là hình chữ nhật (dhnb).
b) Tứ giác AHCE là hình chữ nhật (cmt).
=> AE // HC (Tính chất hình chữ nhật).
Xét tứ giác AEHI có:
+ AE // IH (do AE // HC).
+ AI // EH (gt).
=> Tứ giác AEHI là hình bình hành (dhnb).
c) Ta có: AE = IH (Tứ giác AEHI là hình bình hành).
Mà AE = HC (Tứ giác AHCE là hình chữ nhật).
=> IH = HC.
=> H là trung điểm IC.
Xét tứ giác CAIK có:
+ H là trung điểm của IC (cmt).
+ H là trung điểm của AK (AH = HK).
=> Tứ giác CAIK là hình bình hành (dhnb).
Mà AK vuông góc IC (do AH vuông góc BC).
=> Tứ giác CAIK là hình thoi (dhnb).



Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
=>AHCE là hình bình hành
Hình bình hành AHCE có \(\hat{AHC}=90^0\)
nên AHCE là hình chữ nhật