Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
Ta có: MN // BC
=> ^MIB = ^IBC ( so le trong )
Mà ^MBI = ^IBC ( BI phân giác )
=> ^MIB = ^ MBI
=> Tam giác MBI cân tại M
=> MB = MI
Lại có: MN // BC
=> ^NIC = ^ICB ( so le trong )
Mà ^ICN = ^ICB ( Do CI phân giác )
=> ^NIC = ^ICN
=> Tam giác INC cân tại N
=> IN = NC
Ta có: MN = MI + IN
Hay MN = MB + NC
Vậy MN = MB + NC ( đpcm )

Xét ΔDAI có góc DAI=góc DIA(=góc BAI)
nen ΔDAI cân tại D
=>DA=DI
Xét ΔEIB có góc EIB=góc EBI(=góc ABI)
nên ΔEIB cân tại E
=>EB=EI
DE=DI+IE
=>DE=EB+AD

Tham khảo:
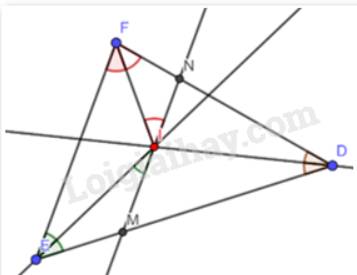
Theo đề bài ta có MN song song với EF
\( \Rightarrow \) \(\widehat {FEI} = \widehat {EIM}\)(2 góc so le trong) và \(\widehat {EFI} = \widehat {FIN}\)(2 góc so le trong)
Xét có \(\widehat {FEI} = \widehat {EIM} = \widehat {IEM}\)(EI là phân giác góc E)cân tại M (2 góc đáy bằng nhau)
\( \Rightarrow \) EM = IM (2 cạnh bên tam giác cân) (1)
Xét có : \(\widehat {EFI} = \widehat {IFN} = \widehat {NIF}\)(FI là phân giác góc F) cân tại N (2 góc đáy bằng nhau)
\( \Rightarrow \)FN = IN (2 cạnh bên tam giác cân) (2)
Ta thấy MN = MI + NI (3)
Từ (1); (2) và (3) \( \Rightarrow \) ME + NF = MN