PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 6 2020
Bài cuối có Max nữa nhé, cần thì ib mình làm cho.
Giả sử \(c=min\left\{a;b;c\right\}\Rightarrow c\le1< 2\Rightarrow2-c>0\)
Ta có:\(P=ab+bc+ca-\frac{1}{2}abc=\frac{ab}{2}\left(2-c\right)+bc+ca\ge0\)
Đẳng thức xảy ra tại \(a=3;b=0;c=0\) và các hoán vị
H
18 tháng 3 2021
Câu 1 :
a)
\(P = a + b - ab = 2 + \sqrt{3} + 2-\sqrt{3} - (2 + \sqrt{3})(2-\sqrt{3})\\ =4 - (2^2 - (\sqrt{3})^2) = 4 - (4 - 3) = 3\)
b)
\(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3x+y=5\\3x-6y=-9\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}y-\left(-6y\right)=5-\left(-9\right)\\x=\dfrac{5-y}{3}\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}y=2\\x=\dfrac{5-2}{3}=1\end{matrix}\right.\)
Vậy nghiệm của hệ phương trình (x ; y) = (1 ; 2)
18 tháng 3 2021
Câu 1:
a)
\(P=a+b-ab\\ =2+\sqrt{3}+2-\sqrt{3}-\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)\\ =4-\left(4-2\sqrt{3}+2\sqrt{3}-3\right)\\ =4-1=3\)
Vậy \(P=3\)
b)
\(\left\{{}\begin{matrix}3x+y=5\\x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6x+2y=10\\x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}7x=7\\x-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\1-2y=-3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\2y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy pht có nghiệm là \(\left(x;y\right)=\left(1;2\right)\)
19 tháng 3 2021
Câu 5 :
Ta chứng minh bđt phụ: \(x^5+y^5\ge xy\left(x^3+y^3\right)\forall x\in N\Leftrightarrow x^5+y^5-x^4y-xy^4\ge0\Leftrightarrow\left(x-y\right)x^4-y^4\left(x-y\right)\ge0\Leftrightarrow\left(x-y\right)\left(x^4-y^4\right)\ge0\Leftrightarrow\left(x-y\right)^2\left(x+y\right)\left(x^2+y^2\right)\ge0\)
\(\Rightarrow x^5+y^5\ge xy\left(x^3+y^3\right)\) (1)
\(x^3+y^3\ge xy\left(x+y\right)\Leftrightarrow\left(x-y\right)^2\left(x+y\right)\ge0\Rightarrow x^3+y^3\ge xy\left(x+y\right)\left(2\right)\)
Áp dụng bđt (1) và (2): \(\Rightarrow\dfrac{ab}{a^5+b^5+ab}\le\dfrac{ab}{ab\left(a^3+b^3\right)+ab}\le\dfrac{ab}{a^2b^2\left(a+b\right)+ab}=\dfrac{1}{ab\left(a+b\right)+1}=\dfrac{abc}{ab\left(a+b+c\right)}=\dfrac{c}{a+b+c}\) Tương tự:
\(\dfrac{bc}{b^5+c^5+bc}\le\dfrac{a}{a+b+c};\dfrac{ca}{c^5+a^5+ca}\le\dfrac{b}{a+b+c}\)
\(\Rightarrow\sum\dfrac{ab}{a^5+b^5+ab}\le\sum\dfrac{c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
Dấu = xảy ra \(\Leftrightarrow a=b=c\)=1
19 tháng 3 2021
Câu 1:
a) Ta có: \(\left(x+3\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=4\\x+3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)
Vậy: S={1;-7}
b) Ta có: \(\left\{{}\begin{matrix}2x+y-3=0\\\dfrac{x}{4}=\dfrac{y}{3}-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=3\\\dfrac{1}{4}x-\dfrac{1}{3}y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+2y=6\\4x-\dfrac{16}{3}y=-16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{22}{3}y=22\\2x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\2x=3-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=3\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(0;3)
B
31 tháng 7 2019
\(a,\)Vì \(a< b\Rightarrow a-b< 0\)
\(\Leftrightarrow\sqrt{a}^2-\sqrt{b}^2< 0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)< 0\)
Mà \(a,b>0\Rightarrow\sqrt{a}+\sqrt{b}>0\)
\(\Rightarrow\sqrt{a}-\sqrt{b}< 0\)
\(\Rightarrow\sqrt{a}< \sqrt{b}\left(đpcm\right)\)
\(b,\)Ta có:\(a\ge0;b>0\Rightarrow\sqrt{a}+\sqrt{b}>0\)
Vì\(\sqrt{a}< \sqrt{b}\Rightarrow\sqrt{a}-\sqrt{b}< 0\)(1)
Nhân hai vế của (1) với \(\sqrt{a}+\sqrt{b}\).Mà theo cmt thì \(\sqrt{a}+\sqrt{b}>0\)nên khi nhân vào thì dấu của BPT (1) không đổi chiều
\(\Rightarrow\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)< 0\left(\sqrt{a}+\sqrt{b}\right)\)
\(\Leftrightarrow\sqrt{a}^2-\sqrt{b}^2< 0\)
\(\Leftrightarrow a-b< 0\)
\(\Rightarrow a< 0\left(đpcm\right)\)
8 tháng 6 2017
Để phương trình đã cho có 2 nghiệm buộc:
\(\Delta\)'\(\ge0\)
\(\Leftrightarrow\left(-m\right)^2+m+3=0\\ \Leftrightarrow\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\veebar m\)
Do đó với mọi m thì phương trình đã cho có 2 nghiệm
Theo hệ thức viet ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1.x_2=\dfrac{c}{a}=-m-3\end{matrix}\right.\)
Từ giả thuyết \(\left|x_1\right|=\left|x_2\right|\\ \Leftrightarrow x_1^2=x_2^2\\ \Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=0\\ \Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}.\left(x_1+x_2\right)=0\)
\(\Leftrightarrow\sqrt{\left(2m\right)^2+4m+12}.2m=0\\ \Leftrightarrow m=0\)(vì căn của 4m^2+4m+12>0)
S
8
22 tháng 1 2019
Đề sai . Với m = n = 1 thì
\(VT-VP=\left|1-\sqrt{2}\right|-\frac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{2}-1-\frac{\sqrt{3}-\sqrt{2}}{3-2}\)
\(=\sqrt{2}-1-\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{2}-\left(1+\sqrt{3}\right)\)
Dễ thấy \(2\sqrt{2}>1+\sqrt{3}\)Nên VT - VP > 0
=> VT > VP
=> Đề sai :3
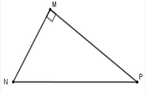
Ta có: cos M N P ^ = M N N P
Đáp án cần chọn là: A