
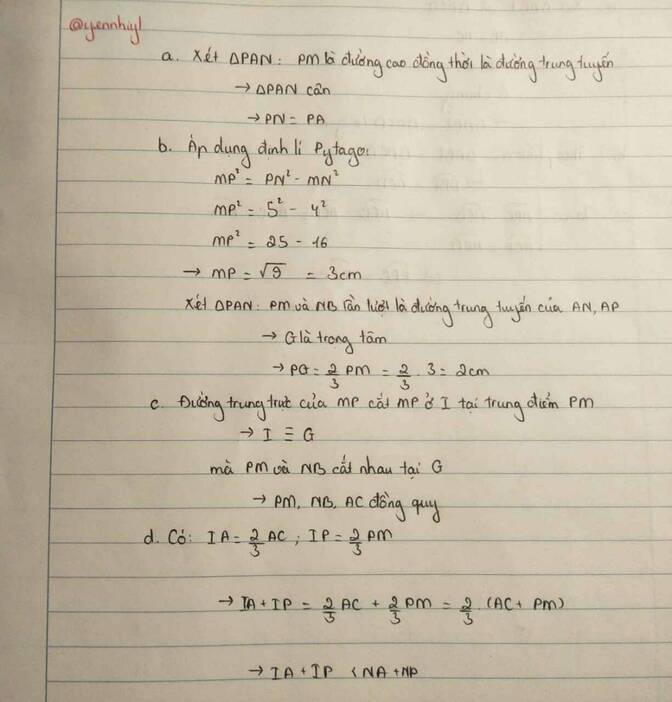
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

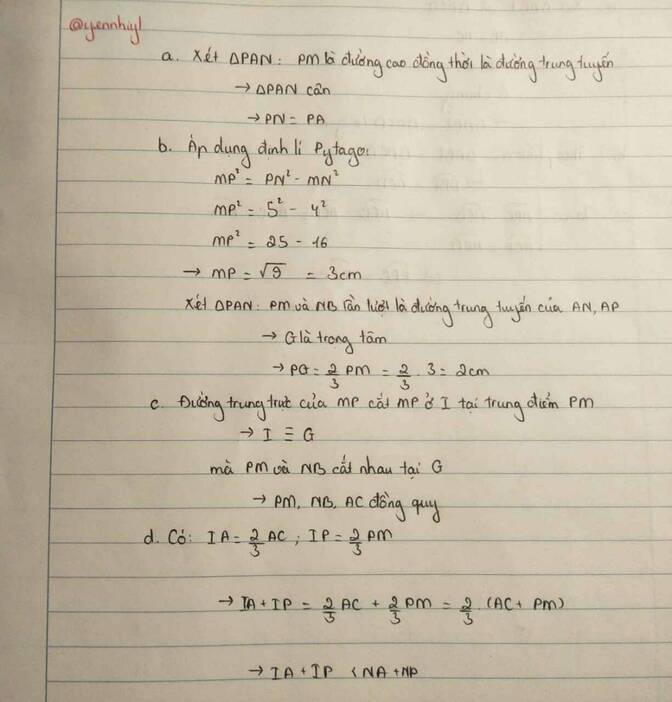

a: Xét ΔPAN có
PM vừa là đường cao, vừa là trung tuyến
=>ΔPAN cân tại P
b: \(PM=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPAN có
NB,PM là trung tuyến
NB cắt PM tại G
=>G là trọng tâm
GP=2/3*3=2cm
c: CI là trung trực của MP
=>I là trung điểm của MP và CI vuông góc MP tại I
Xét ΔMPN có
I là trung điểm của PM
IC//MN
=>C là trung điểm của PN
=>PM,NB,AC đồng quy

a: Xét ΔPAN có
PM là đường trung tuyến
PM là đường cao
DO đó: ΔPAN cân tại P
b: \(MP=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPNA có
PM là đường trung tuyến
NB là đường trung tuyến
PM cắt NB tại G
Do đó; G là trọng tâm của ΔPAN
Suy ra: PG=2/3PM=2(cm)

tự vẽ hình
a)Xét tam giác PMN vuông ở M và tam giác PMA vuông ở M có:
PM:cạnh chung
MN=MA (gt)
=>tam giác PMN=tam giác PMA (2 cạnh góc vuông)
=>PN=PA (cặp cạnh t.ứ)
b)Xét tam giác PMN vuông ở M có:
PM2+MN2=PN2 (Pytago)
=>PM2=PN2-MN2=52-42=9
=>PM=3(cm)
Ta có: MA+MN=AN (M \(\in\) AN),mà MA=MN(gt)
=>M là trung điểm của AN
=>PM là đg trung tuyến ứng với cạnh AN (1)
Vì B là trung điểm của AP (gt)
=>NB là đg trung tuyến ứng với cạnh AP (2)
Từ (1);(2) lại có NB cắt PM tại G
=>G là trọng tâm trong tam giác APM
=>\(GP=\frac{2}{3}PM=\frac{2}{3}.3=2\left(cm\right)\)

a) Xét ΔBNP có
BA là đường trung trực ứng với cạnh PN(gt)
nên ΔBNP cân tại B(Định lí tam giác cân)
b) Xét ΔMBN vuông tại M và ΔCBP vuông tại C có
BN=BP(cmt)
\(\widehat{MBN}=\widehat{CBP}\)(hai góc đối đỉnh)
Do đó: ΔMBN=ΔCBP(cạnh huyền-góc nhọn)

a) Xét \(\Delta\)ANM và \(\Delta\)ABM có :
\(\Rightarrow\)\(\Delta\)ANM = \(\Delta\)ABM ( c . g . c )
\(\Rightarrow\)AN = AB ( hai cạnh tương ứng )
b) Gọi giao điểm giữa NB và MA là I
Xét \(\Delta\)INM và \(\Delta\)IBM có :
\(\Rightarrow\)\(\Delta\)INM = \(\Delta\)IBM ( c . g . c )
\(\Rightarrow\)Góc MIN = góc MIB ( hai góc tương ứng )
Mà góc MIN + góc MIB = 180 ( do kề bù )
nên góc MIN = góc MIB = 180 ÷ 2 = 90 độ hay NB vuông góc với MA .