Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Ta có: MN2+MP2=152+202=625
NP2=252=625
=> MN2+MP2=NP2
=> \(\Delta MNP\)vuông tại M ( theo định lý Py-ta-go đảo)
=> đpcm
b) Ta có I là trung điểm MP
=> \(IM=IP=\frac{MP}{2}=\frac{20}{2}=10\left(cm\right)\)
Xét \(\Delta MNI\)vuông tại M có:
MN2+MI2=NI2 ( theo định lý Py-ta-go)
= 152+102=325
=> NI= \(\sqrt{325}\approx18\left(cm\right)\)
Bài 2:
Xét \(\Delta ABD\)vuông tại D có:
\(AD^2+BD^2=AB^2\)(Theo định lý Py-ta-go)
\(\Rightarrow AD^2+15^2=17^2\)
\(\Rightarrow AD^2=17^2-15^2=64=8^2\)
\(\Rightarrow AD=8\left(cm\right)\)
Lại có: AC=AD+DC
=> 17=8+DC
=> DC=9 cm
Xét \(\Delta BDC\)vuông tại D có:
\(BD^2+DC^2=BC^2\)(Theo định lý Py-ta-go)
\(\Rightarrow BC^2=15^2+9^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17\left(cm\right)\)
Vậy BC\(\approx\)17 cm

Bạn tự vẽ hình nhá :v
a) Ta có : MP - NP < MN < MP + NP
=> 6 < MN < 8
Vì độ dài của đoạn MN là số nguyên nên : MN = 7 ( cm )
b) MN = NP = 7 ( cm )
Nên \(\Delta MNP\) là tam giác cân tại M.
a) Ta có:
MP−NP<MN<MP+NP
⇒6<MN<8⇒6<MN<8
Vì độ dài MNMN là số nguyên nên:
MN=7(cm)MN=7(cm)
b) MN=NP=7(cm)MN=NP=7(cm)
Nên MNPMNP là tam giác cân tại M

Xét tam giác MNP có MN+MP=6+1=7(cm)
Dựa vào bất đẳng thức tam giác =>NP<7cm
Mà NP là số nguyên tố
=>NP thuộc {2;3;5}
Lại có 2+MP=2+1=3<6=MN (ko thỏa mãn BĐT tam giác)
3+MP=3+1=4<6=MN (ko thỏa mãn BĐT tam giác)
5+MP=5+1=6=MN (ko thỏa mãn BĐT tam giác)
=>ko tồn tại tam giác MNP có độ dài như vậy
hay ko tìm được độ dài cưa NP
Bạn xem lại đề đi nhé! ^_^

`\color{blue}\text {#DuyNam}`
Gọi độ dài cạnh còn lại của Tam giác `MNP` là `x (x \ne 0)`
Theo bất đẳng thức trong tam giác ta có:
`MN+MP>x>MN-MP`
`-> 9 cm > x > 3 cm`
`-> x={ 8,7,6,5,4 cm}`
Mà `x` là một số nguyên chia hết cho `5 -> x= 5 (cm)`
cho tam giác mnp có mn= 4cm np=1cm và độ dài của canhk mp là một số nguyên (cm). tính độ dài cạnh mp

có : MN+NP < MP < MN-NP ( Bất đẳng thức tam giác )
4+1 < MP < 4-1
5 < MP < 3
=> MP =4 ( cm)

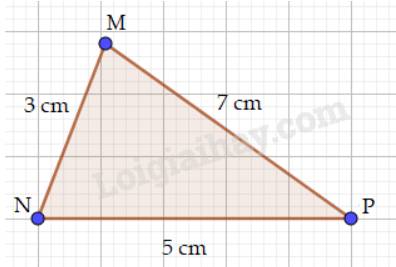
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

Gọi các cạnh tương ứng với các đường cao 3 cm; 4cm; 6 cm là a, b, c ( >0; cm )
Ta có: Diện tích của tam giác là:
\(\frac{1}{2}.3.a=\frac{1}{2}.4.b=\frac{1}{2}.6.c\)
=> \(3a=4b=6c\)
=> \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}\)
Độ dài đường cao tỉ lệ nghịch với độ dài cạnh đáy tương ứng => a là cạnh dài nhất
=> b + c - a = 1
Áp dụng dãy tỉ số bằng nhau ta có: \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}=\frac{b+c-a}{\frac{1}{6}+\frac{1}{4}-\frac{1}{3}}=\frac{1}{\frac{1}{12}}=12\)
=> a = \(\frac{1}{3}.12=4\)cm
b = 3 cm
c = 2 cm
=> Chu vi tam giác là: a + b + c = 4 + 3 + 2 = 9 cm

ABAC=52⇒AB=52ACABAC=52⇒AB=52AC
Áp dụng định lí pytago vào tam giác ABC vuông tại A ta có:
AB2+AC2=BC2AB2+AC2=BC2
=>AB2+AC2=262 (1)
Thay AB=52ACAB=52AC vào (1) ta được:
(52AC)2+AC2=262⇒254AC2+AC2=676(52AC)2+AC2=262⇒254AC2+AC2=676
=>294AC2=676⇒AC2≈93,2⇒AC≈9,7
AB/AC = 5/2 ⇒ AB = 5/2AC
Áp dụng định lí pytago vào tam giác ABC vuông tai A ta có:
\(AB^2+AC^2=BC^2\) \(\Rightarrow\frac{25}{4}AC^2+AC^2=26^2\) \(\Rightarrow\frac{29}{4}AC^2=676\) \(\Rightarrow AC^2\approx93,2\left(cm\right)\)
⇒ AC ≈ 9,7(cm)
=> AB = 5/2 AC = 5/2 . 9,7 = 24,25(cm)
3cm
\(\text{Ta có:MP-MP< MN< MN+MP}\)
\(5-2< MN< 5+2\)
\(3< MN< 7\)
\(\text{Vì NP là 1 số nguyên tố}\)
\(\Rightarrow NP=5\left(cm\right)\)