Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

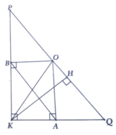
a, Ta có: P K 2 + Q K 2 = 169 = P Q 2
=> ∆KQP vuông tại K
b, Ta có: sin P Q K ^ = P K P Q = 12 13
=> P Q K ^ ≈ 67 0 22 '
=> K P Q ^ = 90 0 - 67 0 22 ' = 22 0 38 '
Theo hệ thức lượng trong tam giác vuông ta có: KH.PQ = KP.KQ => KH = 60 13 cm
P K 2 = P H . P Q => P H = P K 2 P Q = 144 13 cm
c, Tứ giác AKBO có
A
K
B
^
=
K
A
O
^
=
K
B
O
^
=
90
0
=> AKBO là hình chữ nhật => AB = KO
=> AB = KO ≤ KH => A B m i n = KH <=> AB = KO = KH <=> O ≡ H

Lời giải:
a) Ta thấy: $5^2+12^2=13^2$
$\Leftrightarrow KQ^2+KP^2=QP^2$
$\Rightarrow \triangle KQP$ vuông tại $K$ theo định lý Pitago đảo.
b)
$\sin P=\frac{QK}{QP}=\frac{5}{13}\Rightarrow \widehat{P}\approx 22,62^0$
$\widehat{Q}=90^0-\widehat{P}\approx 67,38^0$
$KH=\frac{2S_{KPQ}}{PQ}=\frac{KQ.KP}{PQ}=\frac{5.12}{13}=\frac{60}{13}$ (cm)
Áp dụng định lý Pitago cho tam giác $HKP$ vuông: $PH=\sqrt{KP^2-KH^2}=\sqrt{12^2-(\frac{60}{13})^2}=\frac{144}{13}$ (cm)
c) Sửa lại: Gọi hình chiếu của O trên KP, KQ lần lượt là M, N. Chứng minh MN=KO.....
Thật vậy. Tứ giác $KNOM$ có 3 góc vuông $\widehat{N}=\widehat{K}=\widehat{M}=90^0$ nên $KNOM$ là hình chữ nhật
$\Rightarrow MN=KO$ (đpcm)
Áp dụng BĐT Cô si ta có:
$S_{KNOM}=KM.KN$
Do $ON\parallel KP, OM\parallel KQ$ nên theo định lý Ta-let ta có:
$\frac{KM}{QO}=\frac{KP}{QP}=\frac{12}{13}$
$\frac{KN}{PO}=\frac{KQ}{PQ}=\frac{5}{13}$
$\Rightarrow KM.KN=\frac{60}{13^2}.OQ.OP\leq \frac{60}{13^2}.\left(\frac{OQ+OP}{2}\right)^2$
(theo BĐT Cô-si)
Hay $KM.KN\leq \frac{60}{13^2}.\frac{PQ^2}{4}=\frac{60}{13^2}.\frac{13^2}{4}=15$
Vậy $S_{KNOM}$ max $=15$ khi $OQ=OP$ hay $O$ là trung điểm của $BC$

a: Xét ΔKQP có \(QP^2=KQ^2+KP^2\)
nên ΔKQP vuông tại K
b: Xét ΔKQP vuông tại K có sin Q=KP/QP=12/13
nên góc Q=67 độ
=>góc P=23 độ
\(KH=\dfrac{12\cdot5}{13}=\dfrac{60}{13}\left(cm\right)\)
c: Xét tứ giác KAOB có góc KAO=góc KBO=góc BKA=90 độ
nên KAOB là hình chữ nhật
=>AB=KO

a: XétΔKQP vuông tại K có sin Q=KP/PQ=12/13
nên góc Q=68 độ
=>góc P=22 dộ
b: Xét tứ giác KAOB có góc KAO=góc KBO=góc AKB=90 độ
nên KAOB là hình chữnhật
Suy ra: KO=AB

a) xét tứ giác ABOC có
\(\widehat{ABO}=\widehat{ACO}=90^0\)(tiếp tuyến AB,AC)
=> tứ giác ABOC nội tiếp
b) Xét tam giác ABH zà tam giác AOB có
\(\hept{\begin{cases}\widehat{ABO}chung\\\widehat{BHA}=\widehat{OBA}=90^0\left(BC\perp CA\left(tựCM\right)\right)\end{cases}}\)
=> \(\Delta ABH~\Delta AOB\left(g.g\right)\)
\(=>\frac{AB}{AO}=\frac{AH}{AB}=>AH.AB=AB.AB\left(1\right)\)
xét tam giác ABD zà tam giác AEB có
\(\widehat{BAE}chung\)
\(\widehat{ABD}=\widehat{BEA}\)(cùng chắn \(\widebat{BD}\))
=> \(\Delta ABD~\Delta AEB\left(g.g\right)\)
\(=>\frac{AB}{AE}=\frac{AD}{AB}=>AE.AD=AB.AB\left(2\right)\)
từ 1 zà 2 suy ra
AH.AO=AE.AD(dpcm)
=>\(\Delta ADH~\Delta AOE\)
\(=>\widehat{DEO}=\widehat{DHA}\)(2 góc tương ứng
lại có
\(\widehat{DHA}+\widehat{DHO}=180^0=>\widehat{DEO}+\widehat{DHO}=180^0\)
=> tứ giác DEOH nội tiếp
c) Có tam giá AOM zuông tại O , OB là đường cao
\(=>\frac{1}{OA^2}+\frac{1}{OM^2}=\frac{1}{OB^2}=\frac{1}{R^2}\)
\(\frac{1}{OA.OM}=\frac{1}{OA}.\frac{1}{OM}\le\frac{1}{\frac{OA^2+OM^2}{2}}=\frac{1}{\frac{R^2}{2}}=\frac{1}{2R^2}\left(a,b\le\frac{a^2+b^2}{2}\right)\)
=>\(OA.OM\ge2R^2=>MinS_{AMN}=2R^2\)
dấu = xảy ra khi OA=OM
=> tam giác OAM zuông cận tại O
=> góc A = độ
bài 2
ra kết quả là \(6\pi m^2\)
nếu cần giải bảo mình

A B C H M N O a
a/ Ta có BH = a-5 = 13-5 = 8 (cm) , CH = a+5 = 13+5 = 18 (cm)
Dễ thấy AMHN là hình chữ nhật => AH = MN
Mặt khác, áp dụng hệ thức về cạnh trong tam giác vuông,ta có : \(AH^2=BH.CH=8.18=144\Rightarrow AH=MN=12\)
b/ Bạn tham khảo ở đây : http://olm.vn/hoi-dap/question/677639.html



ngu
rứi mà ko biết
tau bày cho nè
cc
cc
cc