Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

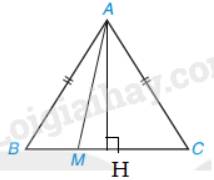
Kẻ AH BC.
a) Trong các đường xiên và đường vuông góc kẻ từ A điểm nằm ngoài đường thẳng BC đến đường thẳng BC thì đường vuông góc là đường ngắn nhất nên AM ngắn nhất khi M trùng H hay M là chân đường vuông góc kẻ từ A đến BC.
b) Cách 1:
+) Khi M trùng H thì AH < AB ( đường vuông góc luôn nhỏ hơn đường xiên)
+) Khi M nằm giữa B và H
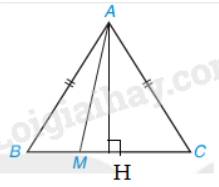
Góc AMB là góc ngoài tại đỉnh M của tam giác AHM nên \(\widehat{AMB}>\widehat{AHM}= 90^0\) nên \(\widehat{AMB}\) là góc tù nên là góc lớn nhất trong tam giác ABM.
Trong tam giác ABM, cạnh AB đối diện với góc lớn nhất nên cạnh AB lớn nhất (định lí). Do đó AM < AB.
+) Khi M nằm giữa C và H
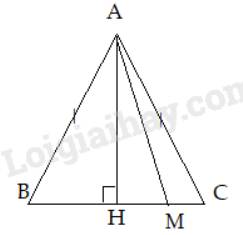
Góc AMC là góc ngoài tại đỉnh M của tam giác AHM nên \(\widehat{AMC}>\widehat{AHM}= 90^0\) nên \(\widehat{AMC}\) là góc tù nên là góc lớn nhất trong tam giác ACM
Trong tam giác ACM, cạnh AC đối diện với góc lớn nhất nên cạnh AC lớn nhất (định lí). Do đó AM < AC.
Mà AB = AC (gt)
\(\Rightarrow \) AM < AB
Vậy AM < AB
Cách 2:
Theo thử thách nhỏ trang 64, khi M thay đổi trên BC, M càng xa H thì AM càng lớn lên. Tuy nhiên, M nằm giữa B và C nên AM không vượt quá AB. Như vậy, AM < AB

a) vì I và E là hình chiếu => góc MIA= góc MKA=90 đô.Rui cm tam giác DIA =tam giác MIA(c-g-c).
b)tam giác MKC= tam giác CKE(c-g-c)
c)tam giác DIA=tam giác MIA> góc DAI= góc MAI=> góc DAI+MAK=90 độ( vì góc IAM+góc MAK=90 độ) tương tự Cm góc EAK+ óc MAI=90 độ Nên góc DAI+IAM+MAK+KAE= 180 độ<=> DAE thẳng hàng
d)CM BD//AM rùi CM AM//CE<=> BD//CE

A C D B L I K J
a, xét tam giác ALI và tam giác ALD có : AL chung
DL = LI (gt)
^ALD = ^ALI = 90
=> tam giác ALI = tam giác ALD (2cgv)
=> AI = AD
tương tự cm được tam giác AKD = tam giác AKJ (2cgv) => AJ = AD
=> AI = AJ
=> tam giác AIJ cân tại A
a, Vì A thuộc đường trung trực của DI
nên AI = AD
Vì A thuộc đường trung trực của DJ nên AJ = AD
Do đó: AI=AJ hay \(\Delta\) AIJ cân tại A
b, ALI = ALD ( c.c.c )
=> AKD = AKJ ( c.c.c )
=> AIJ cân ( cmt )
=> DA là tia p/g của LDK
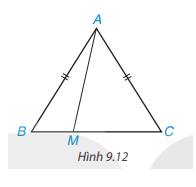
Gọi A là trung điểm của KL
ΔIKL cân tại I
mà IA là đường trung tuyến
nên IA\(\perp\)KL
Khi M thay đổi trên KL, ta luôn có: IA<=IM(quan hệ giữa đường xiên và hình chiếu)
Dấu '=' xảy ra khi A trùng với M
vậy: IM nhỏ nhất khi M là trung điểm của KL