Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vậy bây giờ chị có nhớ cách giải nữa không vậy ? Chị bày cho em với ạ.

xét tam giác ABD có
[laTEX]\frac{AB}{sin 90} = \frac{AD}{sin 36} \Rightarrow AD = sin 36. AB[/laTEX]
xét tam giác ABE có
[laTEX]\frac{AB}{sin 54} = \frac{BE}{sin 108} \Rightarrow BE = \frac{sin 108}{sin 54}. AB[/laTEX]
ta có
[laTEX]sin 108 = sin (2.54) = 2sin 54. cos 54 \\ \\ BE = \frac{2sin 54. cos 54 }{sin 54}.AB = 2cos54.AB[/laTEX]
mặt khác
[laTEX]cos 54 = sin 36 \Rightarrow 2AD = BE[/laTEX]

a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O
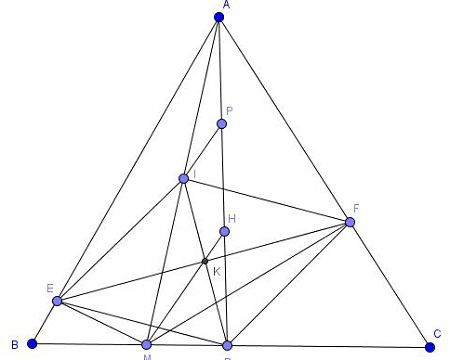
a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O
bạn ơi đề bài sai bạn ơi làm ơn cho mình xin cái đề đúng với
đề này đúng đó