Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(AB=BC=CA=a\)
Gọi D là trung điểm BC \(\Rightarrow AG=BG=\dfrac{2}{3}AD\) và \(DG=\dfrac{1}{3}AD\)
G là trung điểm AK \(\Rightarrow GK=AG=\dfrac{2}{3}AD\Rightarrow GK=BG\) (1)
\(DG+DK=GK\Rightarrow DK=GK-DG=\dfrac{1}{3}AD\Rightarrow DK=DG\) \(\Rightarrow\) BD là trung tuyến của tam giác BGK
Mặt khác tam giác ABC đều \(\Rightarrow AD\perp BC\) \(\Rightarrow\) BD là đường cao của tam giác BGK
Xét tam giác BGK có BD đồng thời là trung tuyến và đường cao
\(\Rightarrow\Delta BGK\) cân tại B \(\Rightarrow BG=BK\) (2)
Từ (1), (2) \(\Rightarrow BG=BK=GK\Rightarrow\Delta BGK\) là tam giác đều


Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

Ta có: GM = MD (chứng minh trên)
Suy ra BM là đường trung tuyến của tam giác BGD.
Suy ra: BM = 1/2 BC (4)
Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:
FG = 1/2 BG (tính chất đường trung tuyến)
GN = 1/2 GB (tính chất đường trung tuyến)
Suy ra: FG = GN
Xét ΔDFG và ΔANG, ta có:
AG = GD (gt)
∠(DGF) = ∠(AGN) (đối đỉnh)
GF = GN (chứng minh trên)
Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN
Mà AN = 1/2 AC (gt)
Suy ra: DF = 1/2 AC (5)
Mặt khác: BD = CG (chứng minh trên)
ED = 1/2 BD (vì E là trung điểm BD)
GP = 1/2 CG (tính chất đường trung tuyến)
Suy ra: ED = GP
Lại có: ΔBMD = ΔCMG (chứng minh trên)
⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)
(CGM) = (PGA) (đối đỉnh)
Suy ra: ∠(EDG) = ∠(PGA)
AG = GD (gt)
Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)
Do đó: GE = 1/2 AB (6)
Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

tự vẽ hình
a) xét tam giác ABD và tam giác AED có:
AB=AE (gt)
góc A1 = góc A2 ( AD là p/giác của góc A)
AD chung
=> tam giác ABD = tam giác AED
câu d) mới hok hồi sáng giờ mk chưa bít vận dụng hết hì để xem lại bài đã mk giải cho
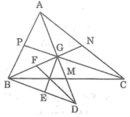
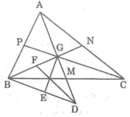
Gọi M là giao điểm AG và BC.
Ta có AG =BG=CG (=2/3 AM) (3 trung tuyến của t.giác đều thì bằng nhau)
Mà AG=GD(gt) => tgiác BGD cân tại G (1)
Mặt khác tam giác BDG có BM là trung tuyến cũng là trung trực nên cân tại B (2)
Từ (1) và (2) => tgiac BDG đều
Cho mình hỏi là còn cách giải khác mà ko xài đường trung trực ko??