Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(T=\overrightarrow{GA}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)+\overrightarrow{GB}.\overrightarrow{CA}+\overrightarrow{GC}.\overrightarrow{AB}\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}-\overrightarrow{GA}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}-\overrightarrow{GB}\right)\)
\(=\overrightarrow{AB}\left(\overrightarrow{GC}+\overrightarrow{AG}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}+\overrightarrow{BG}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{BA}\)
\(=0\)

Chọn C.
Vì ![]() nên
nên
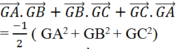
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
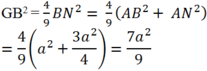
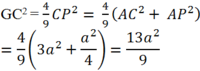
Suy ra
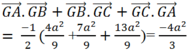

* cái này là công thức rồi bn o cần chứng minh đâu
công thức : cho tam giác ABC ; nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Gọi M trung điểm BC
G đối xứng D qua M
=> tứ giác BGCD là hình bình hành
=> GD=2.GM (Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mà AG = 2.GM ( \(\dfrac{AG}{GM}=\dfrac{2}{1},GA=\dfrac{2}{3}AM\) )
⇒ AG=GD
Mặt khác, G ϵ AD
⇒\(\overrightarrow{AG}=\overrightarrow{GD}\)
Ta có \(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GD}\) (Quy tắc hình bình hành)
Nên \(\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}\) = \(\overrightarrow{GD}+\overrightarrow{GA}\)
Mà \(\overrightarrow{AG}=\overrightarrow{GD}\) (cmt)
⇒\(\overrightarrow{AG}+\overrightarrow{GA}=\overrightarrow{AG}-\overrightarrow{AG}=\overrightarrow{O}\)

Ta đã biết nếu G' là trọng tâm tam giác ABC thì:
\(\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\).
Gỉa sử có điểm G thỏa mãn: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta sẽ chứng minh \(G\equiv G'\).
Thật vậy:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}+\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GG'}=\overrightarrow{0}\).
Vậy \(G\equiv G'\).

Gọi cạnh của tam giác là a
\(GB=GC=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý cosin cho tam giác BCG:
\(cos\widehat{BGC}=\dfrac{GB^2+GC^2-BC^2}{2GB.GC}=\dfrac{2.\left(\dfrac{a\sqrt{3}}{3}\right)^2-a^2}{2\left(\dfrac{a\sqrt{3}}{3}\right)^2}=-\dfrac{1}{2}\)
\(\Rightarrow\widehat{BGC}=120^0\)