Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: IK//DH
a: Xét ΔDEF vuông tại D và ΔHED vuông tại H có
góc E chung
=>ΔDEF đồng dạng với ΔHED
=>DF/DH=EF/DE=DE/HE
=>EH*EF=ED^2
b: Xét ΔFIK vuông tại I và ΔFDE vuông tại D có
góc F chung
=>ΔFIK đồng dạng với ΔFDE
=>FI/FD=FK/FE
=>FI*FE=FK*FD
c: góc KDE+góc KIE=180 độ
=>KDEI nội tiếp
=>góc DKE=góc DIE và góc DEK=góc DIK
mà góc DIE=góc DIK
nên góc DKE=góc DEK
=>ΔDEK cân tại D

a, Vì DH là đường cao (gt) \(\Rightarrow\widehat{DHF}=90^0\)
Xét \(\Delta DEF\)và \(\Delta HDF\)có
\(\widehat{F}\)chung
\(\widehat{EDF}=\widehat{DHF}\left(=90^0\right)\)
\(\Rightarrow\Delta DEF\infty\Delta HDF\left(g-g\right)\)
b, Xét \(\Delta DEF\)vuông tại D , DH là đường cao có
\(HD^2=HE.HF\)(Hệ thức lượng trong tam giác vuông )
c, Xét \(\Delta DEF\)vuông tại D có
\(EF^2=DE^2+DF^2\)(định lí Pytago)
\(25=DE^2+20^2\)
\(625=DE^2+400\)
\(DE^2=225\Rightarrow DE=15\left(cm\right)\)
Xét \(\Delta DEF\)vuông tại , DH là đường cao có
\(DE.DF=EF.DH\)(hệ thức lượng trong tam giác vuông )
\(\Leftrightarrow15.20=25.DH\)
\(\Leftrightarrow DH=\frac{15.20}{25}=12\left(cm\right)\)
d,Xét \(\Delta DEF\)vuông tại D, DH là đường cao có
\(DF^2=FH.FE\) (hệ thức lượng trong tam giác vuông ) (1)
Xét \(\Delta DBF\)vuông tại D , \(DM\perp BF\)có
\(DF^2=FM.FB\)(hệ thức lượng trong tam giác vuông ) (2)
Từ (1) và (2) \(\Rightarrow FH.FE=FM.FB\)
\(\Leftrightarrow\frac{FH}{FB}=\frac{FM}{FE}\)
Xét \(\Delta MHF\)và \(\Delta BEF\)có
\(\widehat{EFB}\)chung
\(\frac{FH}{FB}=\frac{FM}{FE}\left(cmt\right)\)
\(\Rightarrow\Delta MHF\infty\Delta BEF\left(c-g-c\right)\)
Nhớ k cho mình nha

Vì \(DH \bot EF \Rightarrow \widehat {DHE} = 90^\circ \)
Xét tam giác \(DEH\) và tam giác \(FDE\) ta có:
\(\widehat E\) chung
\(\widehat {DHE} = \widehat {EDF} = 90^\circ \).
Do đó, \(\Delta DEH\backsim\Delta FED\) (g.g)
Suy ra, \(\frac{{DE}}{{EF}} = \frac{{EH}}{{DE}} \Rightarrow D{E^2} = EF.EH\) (điều phải chứng minh).

a) xét ΔHED và ΔDEF có
\(\widehat{EHD}=\widehat{EDF}=\)90o
\(\widehat{E} chung\)
=> ΔHED ∼ ΔDEF (gg)
b) Xét ΔDEF có \(\widehat{D}=\)90o
=> DE2+DF2=EF2
=>62+82=EF2
=> EF=10 cm
SΔDEF=\(\dfrac{ED.DF}{2}=\dfrac{DH.EF}{2}\)=> ED.DF=DH.EF => 6.8=DH.10
=> DH =4,8 cm
c) Xét ΔDEH có \(\widehat{EHD}=90\)o
=> HD2.HE2=ED2
=>4.82+HE2=62
=> HE=3.6
ta lại có DI là phân giác
=> \(\dfrac{EI}{IH}=\dfrac{ED}{HD}\)
=>\(\dfrac{EI}{EH-EI}=\dfrac{6}{4.8} \)=>\(\dfrac{EI}{3.6-EI}=\dfrac{6}{4.8}\)=>EI=2
=> IH=EH-EI=3.6-2=1.6
a) Xét ΔHED vuông tại H và ΔDEF vuông tại D có
\(\widehat{HED}\) chung
Do đó: ΔHED\(\sim\)ΔDEF(g-g)

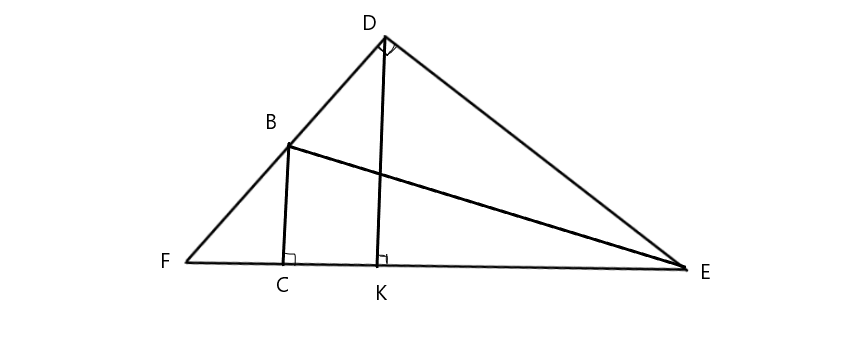
a) Xét Δ DEF vuông tại D ( gt ) có:
∠ DFE + ∠ DEF = 90o ( Tổng 2 góc nọn trong Δ vuông)
Tương tự, ta có :
∠ DFK + ∠ KDF = 90o
=> ∠ KDF = ∠ DEF
Xét Δ KDE và Δ DFE có:
∠ KDF = ∠ DEF (cmt)
∠ DKE = ∠ EDF ( = 90o )
=> Δ KDE ∞ Δ DFE
b) Tương tự, ta có
Δ KFD ∞ Δ DFE
=> Δ KFD ∞ Δ KDE
=> \(\dfrac{DK}{KE}\)= \(\dfrac{KF}{DK}\)
=> DK2 = KE.KF

a) Xét ΔDEN vuông tại N và ΔDFM vuông tại M có
DE=DF(ΔDEF cân tại D)
\(\widehat{EDN}\) chung
Do đó: ΔDEN=ΔDFM(cạnh huyền-góc nhọn)
Suy ra: DN=DM(hai cạnh tương ứng)
Xét ΔDEF có
\(\dfrac{DM}{DE}=\dfrac{DN}{DF}\left(DM=DN;DE=DF\right)\)
nên MN//EF(Định lí Ta lét đảo)
Xét tứ giác EMNF có MN//EF(Cmt)
nên EMNF là hình thang
mà \(\widehat{MEF}=\widehat{NFE}\)(ΔDEF cân tại D)
nên EMNF là hình thang cân
b) Xét ΔDMH vuông tại M và ΔDNH vuông tại N có
DH chung
DM=DN(cmt)
Do đó: ΔDMH=ΔDNH(cạnh huyền-cạnh góc vuông)
c) Ta có: ΔDMH=ΔDNH(cmt)
nên HM=HN(hai cạnh tương ứng)
Ta có: DM=DN(cmt)
nên D nằm trên đường trung trực của MN(1)
Ta có: HM=HN(cmt)
nên H nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra DH là đường trung trực của MN
hay DH\(\perp\)MN

a: \(DE=\sqrt{15^2-12^2}=9\left(cm\right)\)
\(S_{DEF}=\dfrac{1}{2}\cdot9\cdot12=6\cdot9=54\left(cm^2\right)\)
b: Xét tứ giác DMHN có
góc DMH=góc DNH=góc MDN=90 độ
nên DMHN là hình chữ nhật
c: Xét tứ giác DHMK có
DK//MH
DK=MH
Do đó: DHMK là hình bình hành

a) Xét ΔDEF vuông tại D và ΔHED vuông tại H có
\(\widehat{E}\) chung
Do đó: ΔDEF\(\sim\)ΔHED(g-g)
b) Ta có: ΔDEF\(\sim\)ΔHED(cmt)
nên \(\dfrac{DE}{HE}=\dfrac{EF}{ED}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(DE^2=EF\cdot EH\)(đpcm)