Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề sai ! b) CM : FI \(\perp\)DE
Trên mạng có lời giải nhé ! câu lên đó tham khảo
nếu k tìm thấy, ib mik, mik sẽ đưa link
B/ ĐỀ SAI. chứng minh FI vuông góc với DE
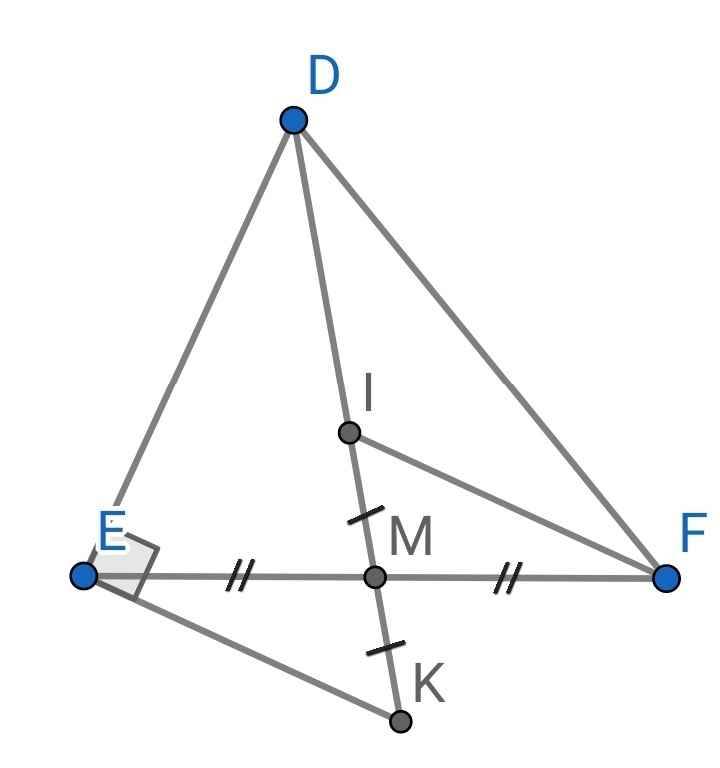
D E F I M K
Xét tam giác EMK và tam giác FMI
có ME=MF (GT)
góc EMK = góc FMI (đối đỉnh)
MI=MK (GT)
suy ra tam giác EMK = tam giác FMI (c.g.c) (1)
b) Từ (1) suy ra góc IFE = góc KEM (2 góc tương ứng) (2)
mà góc IFE ở vị trí so le trong với góc KEM (3)
Từ(2) và (3) suy ra EK // FI (4)
mà EK \(\perp\)DE (GT) (5)
Từ (4) và (5) suy ra FI \(\perp\)DE

a) Xét 2 \(\Delta\) \(EMK\) và \(FMI\) có:
\(EM=FM\) (vì M là trung điểm của \(EF\))
\(\widehat{EMK}=\widehat{FMI}\) (vì 2 góc đối đỉnh)
\(MK=MI\left(gt\right)\)
=> \(\Delta EMK=\Delta FMI\left(c-g-c\right).\)
b) Theo câu a) ta có \(\Delta EMK=\Delta FMI.\)
=> \(\widehat{MEK}=\widehat{MFI}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(EK\) // \(FI.\)
Lại có \(EK\perp DE\left(gt\right)\)
=> \(FI\perp DE\left(đpcm\right).\)
Chúc bạn học tốt!

 a) Do M là trung điểm của EF (gt)
a) Do M là trung điểm của EF (gt)
⇒ ME = MF
Xét ∆EMK và ∆FMI có:
ME = MF (cmt)
∠EMK = ∠FMI (đối đỉnh)
MK = MI (gt)
⇒ ∆EMK = ∆FMI (c-g-c)
b) Do ∆EMK = ∆FMI (gt)
⇒ ∠MEK = ∠MFI (hai góc tương ứng)
Mà ∠MEK và ∠MFI là hai góc so le trong
⇒ EK // FI
Mà EK ⊥ DE (gt)
⇒ FI ⊥ DE

a)Xét\(\Delta DEF\)có:\(EF^2=DE^2+DF^2\)(Định lý Py-ta-go)
hay\(5^2=3^2+DF^2\)
\(\Rightarrow DF^2=5^2-3^2=25-9=16\)
\(\Rightarrow DF=\sqrt{16}=4\left(cm\right)\)
Ta có:\(DE=3cm\)
\(DF=4cm\)
\(EF=5cm\)
\(\Rightarrow DE< DF< EF\)hay\(3< 4< 5\)
b)Xét\(\Delta DEF\)và\(\Delta DKF\)có:
\(DE=DK\)(\(D\)là trung điểm của\(EK\))
\(\widehat{EDF}=\widehat{KDF}\left(=90^o\right)\)
\(DF\)là cạnh chung
Do đó:\(\Delta DEF=\Delta DKF\)(c-g-c)
\(\Rightarrow EF=KF\)(2 cạnh t/ứ)
Xét\(\Delta KEF\)có:\(EF=KF\left(cmt\right)\)
Do đó:\(\Delta KEF\)cân tại\(F\)(Định nghĩa\(\Delta\)cân)
c)Ta có:\(DF\)cắt\(EK\)tại\(D\)là trung điểm của\(EK\Rightarrow DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)cắt\(EF\)tại\(I\)là trung điểm của\(EF\Rightarrow KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
Ta lại có:\(DF\)cắt\(KI\)tại\(G\)
mà\(DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
\(\Rightarrow G\)là trọng tâm của\(\Delta KEF\)
\(\Rightarrow GF=\frac{2}{3}DF\)(Định lí về TC của 3 đg trung tuyến của 1\(\Delta\))
\(=\frac{2}{3}.4=\frac{8}{3}\approx2,7\left(cm\right)\)
Vậy\(GF\approx2,7cm\)
Lời giải:
a) $M$ là trung điểm $EF$ nên \(ME=MF\)
Xét tam giác $EMK$ và $FMI$ có:
\(\left\{\begin{matrix} EM=FM(gt)\\ MK=MI(gt)\\ \widehat{EMK}=\widehat{FMI}(\text{đối đỉnh})\end{matrix}\right.\) \(\Rightarrow \triangle EMK=\triangle FMI(c.g.c)\)
b)
Vì \(\triangle EMK=\triangle FMI\Rightarrow \widehat{MEK}=\widehat{MFI}\)
Mà hai góc này ở vị trí so le trong nên \(EK\parallel FI\)
Mà \(EK\perp DE\)
Suy ra \(FI\perp DE\) (đpcm)