Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~

a) + Δ ABC vuông tại A, có 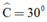
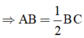
(Trong một tam giác vuông, cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
+ Δ ABC có BD là phân giác của 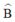
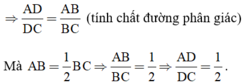
b) AB = 12,5cm ⇒ BC = 2AB = 2.12,5 = 25cm
Áp dụng định lí Py- ta- go vào tam giác ABC ta có:
AB2 + AC2 = BC2 nên AC2 = BC2 - AB2
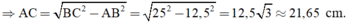
+ Chu vi tam giác ABC là:
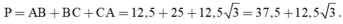
+ Diện tích tam giác ABC là:
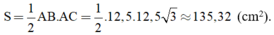

a) Xét ΔABC vuông tại A có \(\widehat{C}=30^0\)(gt)
mà cạnh đối diện với \(\widehat{C}\)
nên \(\dfrac{AB}{BC}=\dfrac{1}{2}\)(Định lí)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{AD}{CD}=\dfrac{1}{2}\)
b) Ta có: \(BC=2\cdot AB\)(cmt)
nên \(BC=2\cdot12.5=25\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=25^2-12.5^2=468.75\)
hay \(AC=\dfrac{25\sqrt{3}}{2}cm\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot\dfrac{25\sqrt{3}}{2}}{2}=\dfrac{150\sqrt{3}}{2}=75\sqrt{3}\left(cm^2\right)\)

a) tg ABD vuong tai A có BD = 2AD (vi góc D=60; C=30)
mà CD=BD ( vì tg CDB cân tại C: có C = B = 30)
VẬY tỷ số AD/CD = BD/CD = 1/2
b) tg ABC = 1/2 TG ĐỀU mà AB=12,5 => BC= 12,5.2 = 25cm
AC = BC\(\sqrt{3}\)/2= 15CĂN3
S= 1/2 . AB.AC = 1/2 , 12,5 . 15căn3 = 93,75\(\sqrt{3}\)cm2
chu vi tg là; 15căn3 + 25+12,5
tôi đã hoàn thành nhiệm vụ, thưa ngài

Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
Vì tổng 2 cạnh luôn lớn hơn 1 cạnh nên. ∆ cân tại C CA = 10
chu vi = 10+10+4=24
h2 =102 - 22 suy ra h=4√6
Diện tích = (4×4√6 )/2 = 8√6
Tam giác cân tại điểm nào bạn?