Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B M D H E F K
câu a Do tam giác AFE có AH vừa là tia phân giác vừa là đường cao nên AFE cân tại A
b. Do KB song song với FE mà tam giác AFE cân tại A nên AKB cũng cân tại A
do đó KF=KA-AF=AB-AE=BE do đó ta có đpcm
c. DO FM//KB mà M lại là trung điểm của BC nên F là trung điểm CK do đó ta có
\(AC+AB=AC+AK=AF-FC+AF+KF=2AF=2AE\)

Ta có hình vẽ
A B c M E F D a)Xét tam giác BEMvà CFMta có
BM=CM(vì AM là trung tuyến ứng với BC)
Góc ABC=góc ACB(vì tam giác ABC cân ở A)
góc BEM=CFM(=90)
=>tam giácBEM=CFM(cạnh huyền-góc nhọn)
b) Từ câu a ta có Tam giác BEM=CFM
=>BE=FC(hai cạnh tương ứng)
ta có AE=AB-BE
AF=AC-CF
Mà AB=AC(tam giác ABC cân ở A)
BE=CF(như trên)
Vậy AE=AF
TRong 1 tam giác cân đường trung tuyến đồng thời là đường phân giác, đường trung trực,....
nên AM là phân giác góc A =>góc BAM=CAM
Xét tam giác AEI và AFI ta có
AI cạnh chung
AE=AF
góc BAM=CAM
=>tam giác AEM=AFM(c.g.c)
=>góc AIE=AIF(tương ứng)
Mà AIE+AIF=180do(kề bù)
=>AIE=AIF=180/2=90do
Vậy AM vuông góc với EF
c) theo câu a ta có tam giác BEM=CFM
=>ME=MF
vậy M thuộc phân giác góc A (1)
Xét tam giác vuông ABD và ACD có
AD cạnh chụng
góc BAM=CAM
=>tam giác ABD=ACD(cạnh huyền -góc nhọn)
=> DB=DC => D thuộc phân giác của góc A(2)
Từ (1) và (2) =>A;M;D thẳng hàng

Bạn tự vẽ hình nha![]()
a.
Xét tam giác EBM vuông tại E và tam giác FCM vuông tại F có:
BM = CM (AM là trung tuyến của tam giác ABC => M là trung điểm của BC)
EBM = FCM (tam giác ABC cân tại A)
=> Tam giác EBM = Tam giác FCM (cạnh huyền - góc nhọn)
b.
AB = AE + EB
AC = AF + FC
mà AB = AC (tam giác ABC cân tại A)
EB = FC (tam giác EBM = tam giác FCM)
=> AE = AF => F thuộc trung trực của EF (1)
mà EM = FM (tam giác EBM = tam giác FCM) => M thuộc trung trực của EF (2)
Từ (1) và (2) => AM là đường trung trực của EF
hay AM _I_ EF
c.
AM là trung tuyến của tam giác ABC cân tại A
=> AM là tia phân giác của BAC (3)
Xét tam giác BAP vuông tại B và tam giác CAP vuông tại Ccó:
AB = AC (tam giác ABC cân tại A)
AP là cạnh chung
=> Tam giác BAP = Tam giác CAP (cạnh huyền - cạnh góc vuông)
=> BP = CP (2 cạnh tương ứng)
=> AP là tia phân giác của BAC
mà AM là tia phân giác của BAC (theo 3)
=> AP \(\equiv\) AM
=. A , P , M thẳng hàng
Chúc bạn học tốt![]()
a) xét tam giác BEM và tam giác CFM có :
góc B = góc C (do tam giác ABC cân tại A)
góc BEM = góc CFM =90 độ
BM = CM (gt)
=> tam giác BEM =tam giác CFM (ch-gn)
=>EM=MF (2 cạnh t ư )
b) gọi I là giao của AM và EF
cm tương tự ta cũng có tam giác AEI= tam giác AFI (c.c.c)
=> EI= IF (2 cạnh t ư )
cm tương tự ta cũng có tam giác EAI = tam giác FAI ( c.g.c )
=> góc EIA = góc FIA ( 2 góc t ư )
mà góc EIA + góc FIA =180 độ
=> góc EIA = góc FIA = 90 độ
=> AM vuông góc vs EF tại I
C) CM : góc AMD = 180 ĐỘ

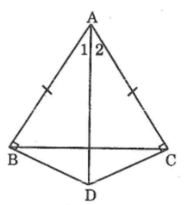
Xét hai tam giác vuông ABD và ACD, ta có:
∠(ABD) =∠(ACD) =90o
Cạnh huyền AD chung
AB = AC (giả thiết)
⇒ ΔABD= ΔACD (cạnh huyền, cạnh góc vuông)
Suy ra: ∠(A1 ) =∠(A2) (hai góc tương ứng)
Suy ra AD là tia phân giác góc A
ea la tia p/g cua BEC