Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình cũng hk pt làm mak thầy cho,neu pn co cau tra loi nho cho minh pt nha

- # Bn có thể gửi từng câu đc ko ? Gửi từng câu thì các bn khác sẽ dễ dàng trl hơn :)
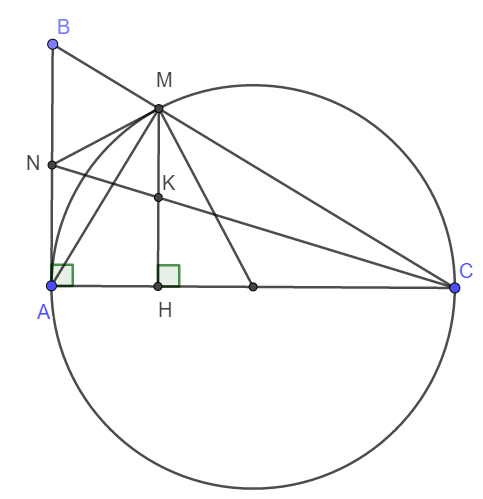
a) Ta thấy ngay \(\widehat{AMC}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat{AMC}=90^o\)
hay tam giác AMC vuông.
b) Ta thấy NA cũng là tiếp tuyến của (O) tại A.
Áp dụng tính chất hai tiếp tuyến cắt nhau, ta có NM = NA.
Xét tam giác vuông ABM có NM = NA nên \(\widehat{NAM}=\widehat{NMA}\Rightarrow\widehat{NBM}=\widehat{NMB}\) (Cùng phụ với hai góc trên)
\(\Rightarrow NM=NB\)
Vậy nên NA = NB.
c) Ta thấy ngay MH // AB nên áp dụng định lý Ta let ta có:
\(\frac{KH}{NA}=\frac{KC}{KN}=\frac{MK}{NB}\)
Lại có NA = NB nên KH = MK hay K là trung điểm MH.

NB^2=NK*NM
=>NB là tiếp tuyến của đường tròn ngoại tiếp ΔMBK
=>NB vuông góc PB
góc DBN=90 độ
=>DB vuông góc NB
=>P,B,D thẳng hàng
Chứng minh tương tự, ta được: C,Q,K thẳng hàng
ΔKPB cân tại P, ΔDBC cân tại D
=>PK//QD
Chứng minh tương tự, ta được: QK//DB
=>DPKQ là hình bình hành
=>DK cắt PQ tại trung điểm của mỗi đường
=>E,D,K thẳng hàng