Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

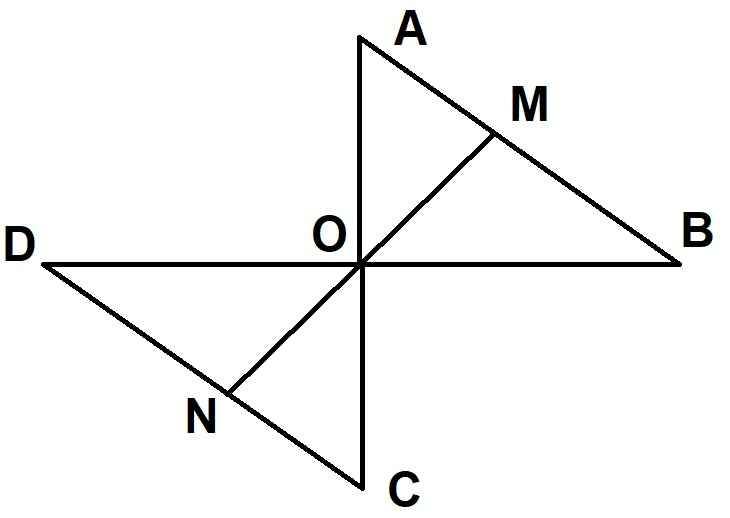
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)
a) xét tam giác AOB và tam giác COD, ta có :
OC = OA (gt)
góc DOC = góc BOA (đối đỉnh)
OD = OB (gt)
=> tam giác AOB = tam giác COD (c.g.c)
b) xét tam giác DON và tam giác BOM, ta có :
OD = OB (gt)
góc DON = góc BOM (đối đỉnh)
MN là cạnh chung
=> tam giác DON = tam giác BOM (c.g.c)
=> MB = ND (2 cạnh tương ứng)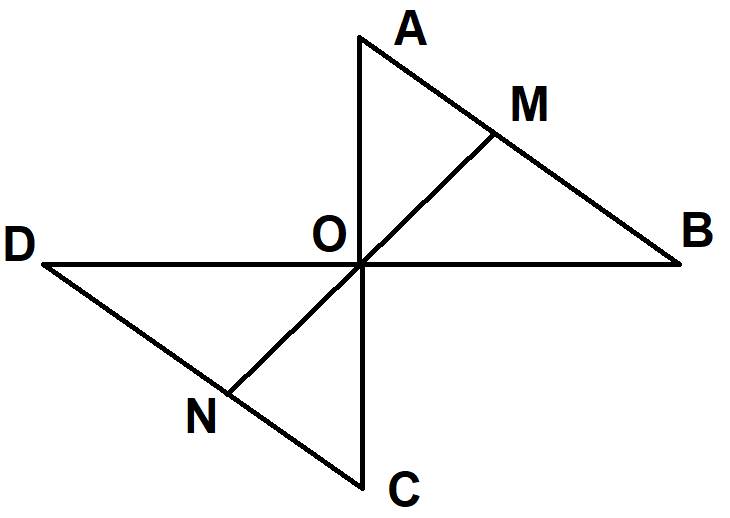

a: Sửa đề: Chứng minh ΔOCD=ΔOAB
Xét ΔOCD và ΔOAB có
OC=OA
\(\widehat{COD}=\widehat{AOB}\)(hai góc đối đỉnh)
OD=OB
Do đó: ΔOCD=ΔOAB
b: Xét ΔBHO vuông tại H và ΔDKO vuông tại K có
BO=DO
\(\widehat{BOH}=\widehat{DOK}\)(hai góc đối đỉnh)
Do đó: ΔBHO=ΔDKO
=>BH=DK
c: ta có;ΔOBA=ΔODC
=>\(\widehat{OBA}=\widehat{ODC}\)
Xét ΔMBO và ΔNDO có
MB=ND
\(\widehat{MBO}=\widehat{NDO}\)
BO=DO
Do đó: ΔMBO=ΔNDO
=>\(\widehat{MOB}=\widehat{NOD}\)
mà \(\widehat{MOB}+\widehat{MOD}=180^0\)(hai góc kề bù)
nên \(\widehat{NOD}+\widehat{MOD}=180^0\)
=>\(\widehat{MON}=180^0\)
=>M,O,N thẳng hàng

a: Sửa đề: Chứng minh ΔOCD=ΔOAB
Xét ΔOCD và ΔOAB có
OC=OA
\(\widehat{COD}=\widehat{AOB}\)(hai góc đối đỉnh)
OD=OB
Do đó: ΔOCD=ΔOAB
b: Xét ΔBHO vuông tại H và ΔDKO vuông tại K có
BO=DO
\(\widehat{BOH}=\widehat{DOK}\)(hai góc đối đỉnh)
Do đó: ΔBHO=ΔDKO
=>BH=DK
c: ta có;ΔOBA=ΔODC
=>\(\widehat{OBA}=\widehat{ODC}\)
Xét ΔMBO và ΔNDO có
MB=ND
\(\widehat{MBO}=\widehat{NDO}\)
BO=DO
Do đó: ΔMBO=ΔNDO
=>\(\widehat{MOB}=\widehat{NOD}\)
mà \(\widehat{MOB}+\widehat{MOD}=180^0\)(hai góc kề bù)
nên \(\widehat{NOD}+\widehat{MOD}=180^0\)
=>\(\widehat{MON}=180^0\)
=>M,O,N thẳng hàng

a) Xét tam giác tam giác ABO và tam giác CDO có:
+ OB = OD (gt).
+ OA = OC (gt).
+ ^AOB = ^COD (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do OA = OC).
+ O là trung điểm của BD (do OB = OD).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do OA = OC).
=> MO là đường trung bình.
=> MO // BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do OB = OD).
=> NO là đường trung bình.
=> NO // BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng (đpcm).

a) Xét tam giác tam giác ABO và tam giác CDO có:
+ \(\text{OB = OD}\) (gt).
+ \(\text{OA = OC }\)(gt).
+ \(\widehat{AOB}\) = \(\widehat{COD}\) (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do \(\text{OA = OC}\)).
+ O là trung điểm của BD (do \(\text{OB = OD}\)).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do \(\text{OA = OC}\)).
=> MO là đường trung bình.
=> MO // BC và MO = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do \(\text{OB = OD}\)).
=> NO là đường trung bình.
=> NO // BC và NO = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng và MO = NO (do cùng = \(\dfrac{1}{2}\) BC).
=> O là trung điểm của MN (đpcm).
a) Xét tam giác tam giác ABO và tam giác CDO có:
+ OB = ODOB = OD (gt).
+ OA = OC OA = OC (gt).
+ ˆAOB���^ = ˆCOD���^ (2 góc đối đỉnh).
=> Tam giác ABO = Tam giác CDO (c - g - c).
b) Xét tứ giác ABCD có:
+ O là trung điểm của AC (do OA = OCOA = OC).
+ O là trung điểm của BD (do OB = ODOB = OD).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> AB // CD (Tính chất hình bình hành).
c) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ O là trung điểm của AC (do OA = OCOA = OC).
=> MO là đường trung bình.
=> MO // BC và MO = 1212 BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác BDC có:
+ N là trung điểm của CD (gt).
+ O là trung điểm của BD (do OB = ODOB = OD).
=> NO là đường trung bình.
=> NO // BC và NO = 1212 BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) => 3 điểm M; O; N thẳng hàng và MO = NO (do cùng = 1212 BC).
=> O là trung điểm của MN (đpcm).
 có đẹp không ạ
có đẹp không ạ 