Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
GIẢI: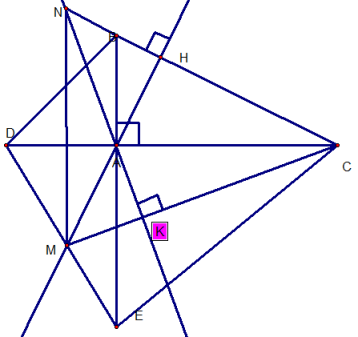
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
a. Gọi G là trung điểm AD
Tam giác ABC đều \(\Rightarrow\widehat{B}=\widehat{C}=60^0\)
\(CD=BC-BD=40\left(cm\right)\)
Trong tam giác vuông BDI:
\(sinB=\dfrac{ID}{BD}\Rightarrow DI=BD.sinB=20.sin60^0=10\sqrt{3}\left(cm\right)\)
\(cosB=\dfrac{IB}{BD}\Rightarrow IB=BD.cosB=20.cos60^0=10\left(cm\right)\)
Trong tam giác vuông CDK:
\(sinC=\dfrac{DK}{CD}\Rightarrow DK=CD.sinC=40.sin60^0=20\sqrt{3}\left(cm\right)\)
\(cosC=\dfrac{KC}{CD}\Rightarrow KC=CD.cosC=40.cos60^0=20\left(cm\right)\)
b. Gọi M là trung điểm BC \(\Rightarrow BM=CM=\dfrac{1}{2}BC=30\left(cm\right)\)
\(DM=BM-BD=10\left(cm\right)\) ; \(AM=\dfrac{AB\sqrt{3}}{2}=30\sqrt{3}\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADM:
\(AD=\sqrt{AM^2+DM^2}=20\sqrt{7}\left(cm\right)\)
\(AG=DG=\dfrac{AD}{2}=10\sqrt{7}\left(cm\right)\)
\(AI=AB-BI=50\left(cm\right)\)
Hai tam giác vuông AEG và ADI đồng dạng (chung góc \(\widehat{IAD}\))
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AG}{AI}\Rightarrow AE=\dfrac{AG.AD}{AI}=28\left(cm\right)\)
Do EG là trung trực AD \(\Rightarrow DE=AE=28\left(cm\right)\)
Tương tự ta có \(AK=AC-CK=40\left(cm\right)\)
Hai tam giác vuông AGF và AKD đồng dạng
\(\Rightarrow\dfrac{AG}{AK}=\dfrac{AF}{AD}\Rightarrow AF=\dfrac{AG.AD}{AK}=35\left(cm\right)\)
\(\Rightarrow DF=AF=35\left(cm\right)\)
\(EF=EG+FG=\sqrt{AE^2-AG^2}+\sqrt{AF^2-AG^2}=7\sqrt{21}\left(cm\right)\)
a: AD=căn 6^2+8^2=10cm
b: Xét ΔBAD vuông tại B có sin BAD=BD/DA=4/5
=>góc BAD=53 độ
Xét ΔBAC vuông tại B có tan BAC=BC/BA=1/2
=>góc BAC=27 độ