Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B O M H I K E N
1) Ta thấy: Tứ giác AHMB nội tiếp đường tròn => ^HAM=^HBM; ^HMA=^HBA
Do H là điểm chính giữa của cung AM nên \(\Delta\)AHM cân tại H => ^HAM=^HMA
Từ đó suy ra: ^HBM=^HBA hay ^HBE=^HBA => BH là phân giác ^ABE
H thuộc nửa đường tròn đường kính AB => AH\(\perp\)BH hay BH\(\perp\)AE
Xét \(\Delta\)BAE: BH là phân giác ^ABE; BH\(\perp\)AE => \(\Delta\)BAE cân đỉnh B (đpcm).
2) Xét \(\Delta\)KHA và \(\Delta\)KAB: ^KHA=^KAB (=900); ^AKB chung => \(\Delta\)KHA ~ \(\Delta\)KAB (g.g)
\(\Rightarrow\frac{KH}{KA}=\frac{KA}{KB}\Rightarrow KH.KB=KA^2\)(1)
Ta có: AE\(\perp\)BK tại H và AH=EH => A đối xứng với E qua BK => AK=KE. Thay vào (1):
\(\Rightarrow KH.KB=KE^2\)(đpcm).
3) Dễ thấy: 2 điểm A và N cùng nằm trên (B) => BA=BN => \(\Delta\)ABN cân đỉnh B
Mà BM\(\perp\)AN => BM là đường trung trực của AN hay BE là trung trực của AN
=> EA=EN => \(\Delta\)AEN cân đỉnh E = >^EAN=^ENA (2)
Lại có: ^HAM=^HBM (Cùng chắn cung HM) hay ^EAN=^EBI (3)
(2); (3) => ^ENA=^EBI hay ^ENI=^EBI => Tứ giác BIEN nội tiếp đường tròn (đpcm).
4) Ta có: ^KAB=900. Mà KA và AB đều cố định
Vậy để ^KAM=900 thì điểm M phải trùng với điểm B.

ban tu ve hinh nhe
Ta co goc AEBnam ngoai dt nen goc AEB = 1/2(CUNG AB-cungHM)=1/2(cungHM+ cung MB)
ma goc Achan cung HB nen AEB=A nen tam giac AEB can o B
ban se de cm duoc AEBK thuoc 1dt nenKEB=90 nen KE^2=KH.KB
xet tam giac AEB co EI la duong cao con lai nenEIM dong dang EAB nenEIM=EBA
ma EBA=MBN nen EIM=MBN
ma EIM VA MBNcung nhin EN nenIENB thuoc 1duong tron

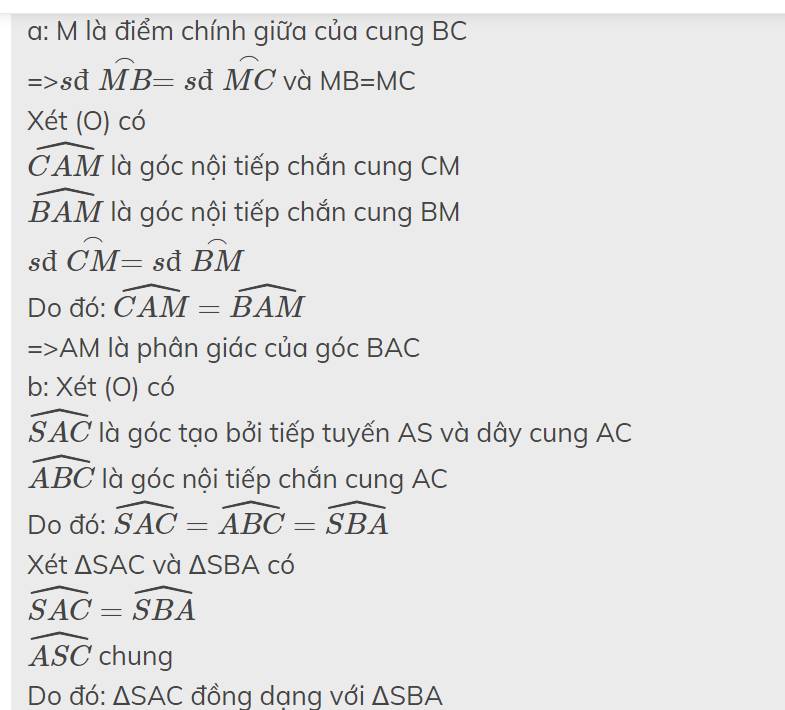


d: \(SA^2=SB\cdot SC\)
\(SE^2=SB\cdot SC\)
=>SA=SE
Xét ΔOAS và ΔOES có
OA=OE
SA=SE
OS chung
Do đó: ΔOAS=ΔOES
=>\(\widehat{OAS}=\widehat{OES}\)
mà \(\widehat{OAS}=90^0\)
nên \(\widehat{OES}=90^0\)
=>E nằm trên đường tròn đường kính SO
mà S,A,O,D cùng thuộc đường tròn đường kính SO(cmt)
nên E nằm trên đường tròn (SAOD)