Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

I là tâm đường tròn nội tiếp tam giác và E là tiếp điểm
nên IE⊥AC, mà A^=90o suy ra IE//AB
⇒ANEI=AMEM
⇒AN=AM.EIEM=AC.EI2(AM−AE) (1)
Tứ giác AEIF là hình vuông nên AE=EI;
D, E, F là các tiếp điểm
⇒AE+CD+BD=12(BC+CA+AB)⇒AE=AC+AB−BC2,
thay vào (1) ta được ...

a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)

M A B C I D N O H K
a) CM: \(\widehat{OBM}=\widehat{ODC}\)
\(\widehat{OBM}+\widehat{OBC}=180^o\)( kề bù)
\(\widehat{ODC}+\widehat{OBC}=180^o\)( tứ giác ODCB nội tiếp )
=> \(\widehat{OBM}=\widehat{ODC}\)
b)
+)Xét tam giác MCN có CO là tia phân giác đồng thời là đường cao
=> Tam giác CMN cân tại C (1)
=> \(\widehat{BMA}=\widehat{DNA}=\widehat{BAM}\)( CD//BA => DN//BA)
=> Tam giác BMA cân tại B
=> BM=BA=CD ( ABCD là hình bình hành) (2)
+) CO là phân giác \(\widehat{BCD}\)
=> \(\widebat{BO}=\widebat{DO}\)
=> BO=DO (3)
+) Xét tam giác BOM và tam giác DOC có:
\(\widehat{OBM}=\widehat{ODC}\)( theo a)
BM=CD ( theo 2)
BO=DO (theo 3)
=> \(\Delta BOM=\Delta DOC\)
+) OM=OC
Và từ (1) => CO là đường trung trực của MN
=> OM=ON
Vậy OM=ON=OC
=> O là tâm đường tròn ngoại tiếp tam giác CMN
c) GỌi H là giao của IO và BD
=> IH vuông BD và H là trung điể m BD
Ta có: \(KD^2=\left(HD-HK\right)^2=HD^2+HK^2-2.HD.HK=ID^2-IH^2+IK^2-IH^2-2HD\left(HD-KD\right)\)
\(=ID^2+IK^2-2\left(IH^2+HD^2\right)+2HD.KD=ID^2+IK^2-2ID^2+2HD.KD\)
\(=IK^2-ID^2+2HD.KD\)
=> \(IB^2-IK^2=ID^2-IK^2=2HD.KD-KD^2\)
=> \(\frac{IB^2-IK^2}{KD^2}=\frac{2HD-KD}{KD}=\frac{BD-KD}{KD}=\frac{BK}{KD}\)(4)
Ta lại có: CK là phân giác trong của tam giác CBD
=> \(\frac{BK}{KD}=\frac{CB}{CD}\)
Và MB=DC ( theo cm câu a) , CM=CN ( Tam giác CMN cân)
=> CB=DN
=> \(\frac{BK}{KD}=\frac{DN}{MB}\)(5)
Từ (4), (5)
=> ĐPCM

A B C T K O P S E F G I
a) Áp dụng tính chất của góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, ta có:
\(\widehat{TAB}=\widehat{TCA}\)
Suy ra \(\Delta\)TAB ~ \(\Delta\)TCA (g.g) \(\Rightarrow\frac{TA}{TC}=\frac{TB}{TA}\Rightarrow TA^2=TB.TC\)(đpcm)
Hai điểm A và K cùng nằm trên (T) nên \(\Delta\)ATK cân tại T => \(\widehat{TAK}=\widehat{TKA}\)(1)
Dễ thấy góc TKA là góc ngoài của \(\Delta\)ACK => \(\widehat{TKA}=\widehat{CAK}+\widehat{ACK}\)
\(\Rightarrow\widehat{CAK}=\widehat{TKA}-\widehat{ACK}\)(2)
Ta có: \(\widehat{BAK}=\widehat{TAK}-\widehat{TAB}=\widehat{TAK}-\widehat{ACB}\)(Do \(\widehat{TAB}=\widehat{ACB}\))
hay \(\widehat{BAK}=\widehat{TAK}-\widehat{ACK}\)(3)
Từ (1); (2) và (3) suy ra: \(\widehat{BAK}=\widehat{CAK}\)=> AK là tia phân giác của \(\widehat{BAC}\)(đpcm).
b) Ta có: \(\frac{TA}{TC}=\frac{TB}{TA}\)=> \(\frac{TP}{TC}=\frac{TB}{TP}\)(P và A thuộc (T))
Từ đó ta chứng minh được: \(\Delta\)TBP ~ \(\Delta\)TPC (c.g.c) => \(\widehat{TPB}=\widehat{TCP}\)
Xét \(\Delta\)BPC: Tia PT nằm ngoài tam giác thỏa mãn \(\widehat{TPB}=\widehat{TCP}\)
Vậy nên TP là tiếp tuyến của đường tròn ngoại tiếp \(\Delta\)BPC (đpcm).
c) Gọi giao điểm của của AT và EF kéo dài là G, EF cắt AP tại điểm I.
Ta thấy tứ giác BEFC nội tiếp (O) => \(\widehat{BCP}=\widehat{EFP}\)hay \(\widehat{EFP}=\widehat{TCP}\)
Mà \(\widehat{TPB}=\widehat{TCP}\)(cmt) => \(\widehat{EFP}=\widehat{TPB}\)
Vì 2 góc trên nằm ở vị trí so le trong nên TP // EF hay TP // GI
Lại có: \(\Delta\)ATP cân tại T có GI // TP (G\(\in\)AT; I\(\in\)AP) => \(\Delta\)AGI cân tại G => \(\widehat{GAI}=\widehat{GIA}\)(4)
\(\widehat{EAI}=\widehat{GAI}-\widehat{GAE}\)(5); \(\widehat{FAI}=\widehat{GIA}-\widehat{AFG}\)(6)
Dễ chứng minh \(\widehat{GAE}=\widehat{AFG}\)(7)
Từ (4); (5); (6) và (7) => \(\widehat{EAI}=\widehat{FAI}\) hay \(\widehat{EAS}=\widehat{FAS}\)
Mà tứ giác AESF nội tiếp (O) => \(\widehat{EAS}=\widehat{EFS}\)và \(\widehat{FAS}=\widehat{FES}\)
Từ đó ta có: \(\widehat{EFS}=\widehat{FES}\)=> Tam giác ESF cân tại S => S nằm trên đường trung trực của EF
Mà EF là dây cung của (O) nên O cũng nằm trên trung trực của EF
Do đó SO là trung trực của EF hay \(SO\perp EF\)(đpcm).
Xin lỗi bạn, 2 góc EFP và TPB là hai góc đồng vị, không phải so le trong nhé.

Ta có: = 2
= 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và =
(đối đỉnh)
mà = 180o -
= 180o - 60o = 120o
nên = 120o (2)
=
+
= 60o + = 60o+ 60o
(sử dụng góc ngoài của tam giác)
Do đó = 120o
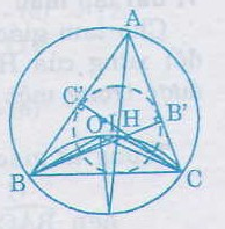
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn
Ta có: \(\widehat{BOC}\) = 2\(\widehat{BAC}\) = 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và \(\widehat{BHC}\) = \(\widehat{B'HC'}\) (đối đỉnh)
mà \(\widehat{B'HC'}\) = 180o - \(\widehat{A}\) = 180o - 60o = 120o
nên \(\widehat{BHC}\) = 120o (2)
\(\widehat{BIC}\) = \(\widehat{A}\) + \(\dfrac{\widehat{B}+\widehat{C}}{2}\)
= 60o + \(\dfrac{180^0-60^0}{2}\) = 60o+ 60o
(sử dụng góc ngoài của tam giác)

Do đó \(\widehat{BIC}\) = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn