Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$|\overrightarrow{BC}|=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$ theo định lý Pitago.

1) Ta có:\(\overrightarrow{AB}+\overrightarrow{DE}-\overrightarrow{DB}+\overrightarrow{BC}=\overrightarrow{AE}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{BE}+\overrightarrow{EC}\)
\(=\overrightarrow{AC}+\overrightarrow{BE}+\overrightarrow{CE}+\overrightarrow{EC}=\overrightarrow{AC}+\overrightarrow{BE}\left(đpcm\right)\)2) a) Ta có: \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\left(đpcm\right)\)
b) Ta có: \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)
\(=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{DB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}\left(đpcm\right)\)c) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AB}-\overrightarrow{BD}\)
\(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}+\overrightarrow{BC}\) ( đề bài bị lỗi gì à ?? :v ) hay do mình =))

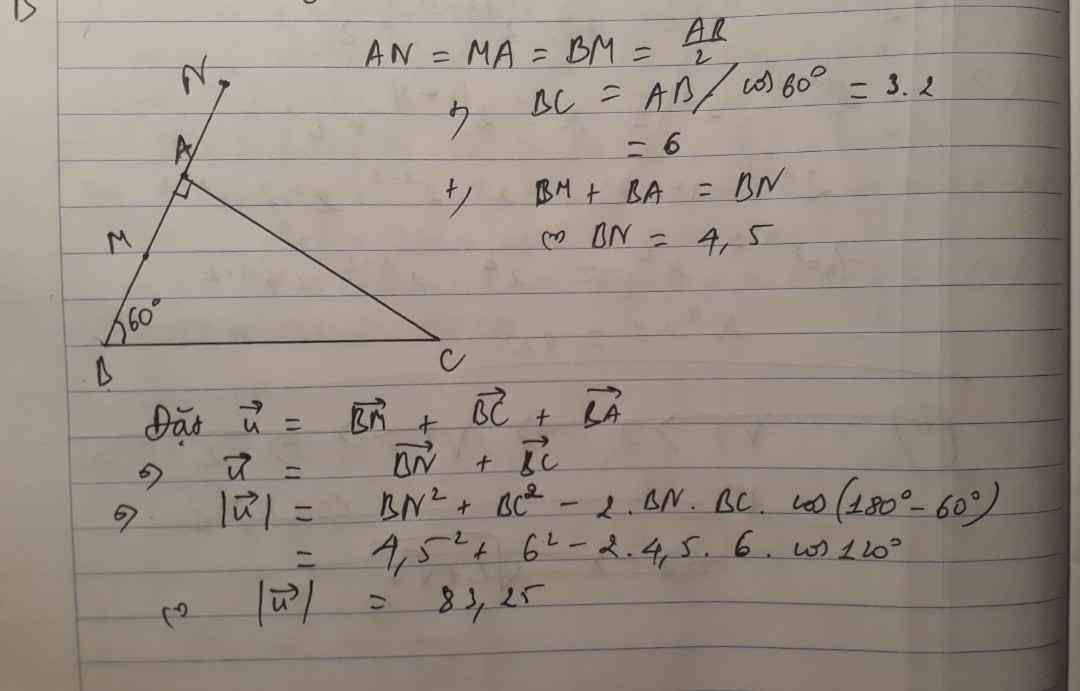
b: \(\left|\overrightarrow{BA}+\overrightarrow{BC}\right|=\left|\dfrac{\overrightarrow{AC}}{2}\right|=\dfrac{5}{2}a\)