Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AB = 3k; AC = 4k . Áp dụng hệ thức lượng vào tam giác vuông ABC thu được k = 3. Từ đó tính được : BH = 5,4cm, HC = 9,6cm

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
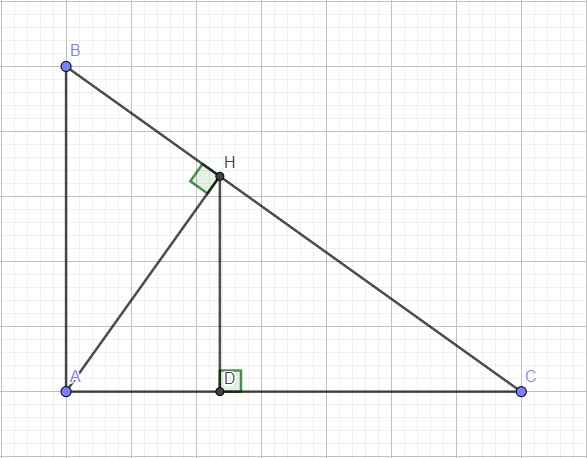
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm

AB/AC=3/4
=>BH/CH=9/16
=>BH/9=CH/16=(BH+CH)/(9+16)=15/25=0,6
=>BH=5,4cm; CH=9,6cm

Áp dụng định lý Pitago cho tam giác vuông ACH:
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC:
\(AC^2=CH.BC\Rightarrow BC=\dfrac{AC^2}{CH}=\dfrac{25}{2}\) (cm)
\(\Rightarrow BH=BC-CH=\dfrac{9}{2}\left(cm\right)\)
Pitago tam giác vuông ABC:
\(AB=\sqrt{BC^2-AC^2}=\dfrac{15}{2}\left(cm\right)\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ACH:
\(HD.AC=AH.HC\Rightarrow HD=\dfrac{AH.HC}{AC}=\dfrac{24}{5}\left(cm\right)\)
Tiếp tục là hệ thức lượng:
\(AH^2=AD.AC\Rightarrow AD=\dfrac{AH^2}{AC}=\dfrac{18}{5}\left(cm\right)\)
\(S_{AHD}=\dfrac{1}{2}AD.HD=\dfrac{216}{25}\left(cm^2\right)\)

Lời giải:
Vì $AB:AC=3:4$ nên đặt $AB=3a, AC=4a$
Theo định lý Pitago:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow (3a)^2+(4a)^2=15^2\)
\(\Leftrightarrow 25a^2=15^2\Rightarrow a^2=9\Rightarrow a=3\)
Do đó \(AB=9; AC=12\) (cm)
Theo hệ thức lượng trong tam giác vuông:
\(AB^2=BH.BC\) (có thể chứng minh bằng \(\triangle BAH\sim \triangle BCA\) )
\(\Rightarrow BH=\frac{AB^2}{BC}=\frac{9^2}{15}=5,4\)(cm)
\(CH=BC-BH=15-5,4=9,6\) (cm)
b)
Theo tính chất phân giác:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}\)
\(\Rightarrow \frac{BD}{BC}=\frac{BD}{BD+DC}=\frac{3}{3+4}=\frac{3}{7}\)
\(\Rightarrow BD=\frac{3}{7}BC=\frac{45}{7}\) (cm)
\(HD=BD-BH=\frac{45}{7}-5,4=\frac{36}{35}\) (cm)
Tuấn Mai: Bạn đọc kỹ phần trên. $AC=4a$. Mà $a=3$ nên $AC=4.3=12$ nhé bạn.