Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : AH2 = BH x HC
=》 256 = 25 x HC
=》 HC = 10,24
BC = BH +HC = 35,24
Lại có : AB\(^2\)= BH x BC
=》 AB2 = 25 x 35,24 = 881
=》 AB = \(\sqrt{ }\)881
Áp dụng định lý Py ta go vào \(\Delta\)ABC có :
AC2 +AB2 = BC2
=》 AC2 = 1241,8576 - 881
=》 AC2 = 360,8576
=》 AC \(\approx\)19
b) Áp dụng định lý Py ta go vào \(\Delta\)ABH có :
AB2 = BH2 + AH2
AH2 = 144 -36
AH = 6\(\sqrt{ }\)3
Lại có : AB2 = BH x BC
144 = 6 x BC
=》 BC = 24
=》 HC = 24 - 6 = 18
Áp dụng định lý Py ta go vào \(\Delta\)ABC có :
AB2 + AC2 = BC2
=》 AC2 = 576 - 144
=》 AC = 12\(\sqrt{ }\)3

a) Áp dụng định lí Py-ta-go vào \(\Delta AHB\) vuông ở \(\widehat{H}\)ta có:
AB2=AH2+BH2
=> AB=\(\sqrt{16^2+25^2}\)
<=>AB=\(\sqrt{881}\)
Áp dụng hệ thức 2 vào \(\Delta ABC\)vuông tại \(\widehat{A}\)ta có:
AH2=BH.CH
<=> 162=25.CH
<=>256=25.CH
=>CH=\(\frac{256}{25}\)=10,24
Ta có:BC=BH+CH
<=>BC=25+\(\frac{256}{25}\)=\(\frac{881}{25}\)=35.24
Áp dụng định lí Py-ta-go vào \(\Delta ABC\)vuông tại \(\widehat{A}\)ta có:
BC2=AB2+AC2
<=>AC2=BC2-AB2
=>AC=\(\sqrt{\left(\sqrt{881}\right)^2-\left(\frac{881}{25}\right)^2}\)=\(-\sqrt{360,8576}\)
b)Áp dụng định lí Py-ta-go vào \(\Delta AHB\)vuông tai \(\widehat{H}\)ta có:
AB2=AH2+BH2
<=>AH2=AB2-BH2
<=>AH=\(\sqrt{12^2-6^2}\)=\(\sqrt{108}\)
Áp dụng hệ thức 2 vào \(\Delta ABC\)vuông tai \(\widehat{A}\)ta có:
AH2=BH.CH
<=>108=36.CH
=>CH=\(\frac{108}{36}\)=3
Ta có:BC=BH+CH
<=> BC=6+3=9
Áp dụng Py-ta-go vào \(\Delta ABC\)vuông tại \(\widehat{A}\)ta có:
BC2=AB2+AC2
<=>AC2=BC2-AB2
=> AC=\(\sqrt{9^2-12^2}\)=\(-\sqrt{63}\)
Nhớ sau mỗi kết quả của phép tính viết "(cùng đơn vị đo)" nhé!

Câu 2:
AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
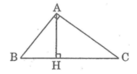
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>900k^2=900
=>k=1
=>HB=25cm; HC=36cm

A C B H
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB = \(\sqrt{881}\)
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC = \(\sqrt{\text{360,8576}}\)

Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH = 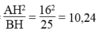
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = ![]()
≈ 29,68
A C 2 = H C . B C
⇒ AC = ![]() ≈ 18,99
≈ 18,99

Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)

a: CH=16^2/25=10,24cm
BC=25+10,24=35,24cm
AB=căn 16^2+25^2=căn 881(cm)
b: AH=căn 12^2-6^2=6căn 3cm
CH=AH^2/HB=108/6=18cm
BC=6+18=24cm
c: BC=căn 5^2+25^2=5 căn 26cm
BH=5^2/5căn 26=5/căn 26(cm)
CH=5căn 26-5/căn 26=24,51(cm)
d: AB=căn 16^2-14^2=2căn15(cm)
e: AB=căn 2*8=4cm
AC=căn 6*8=4căn 3(cm)
