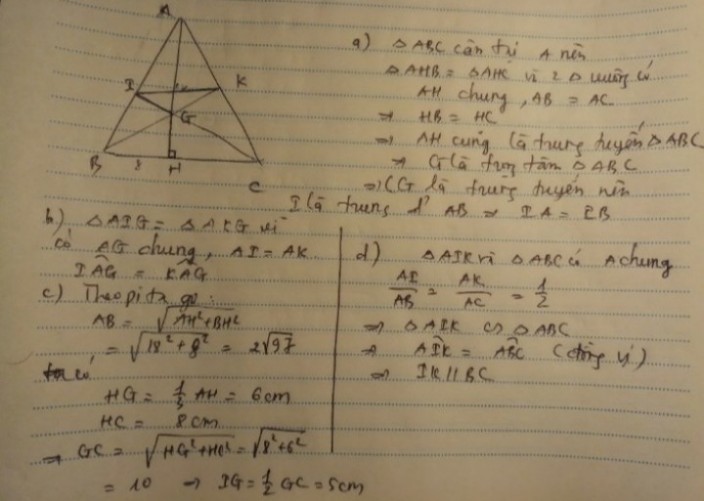Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng ĐL Pytago vào tam giác ABC vuông tại A ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=\sqrt{36}=6\left(cm\right)\)
Có diện tích tam giác ABC \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}AB.AC\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=\frac{48}{10}=4,8\left(cm\right)\)
Áp dụng ĐL Pytago vào tam giác ABH vuông tại H ta có :
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6\left(cm\right)\)
Áp dụng ĐL Pytago vào tam giác ACH vuông tại H ta có :
\(CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4\left(cm\right)\)

Vì G là trọng tâm ΔABC
⇒AG=2323 AH=2323 18=12(cm)
Mà AG=2GH
⇒GH=AG2AG2 =122122 =6(cm)
BH=HC(do AH là trung tuyến BC)
⇒BH=HC=BC2BC2 =162162 =8(cm)
Xét ΔGHC có:
GH²+HC²=GC²(Định lí Pi-ta-go)
⇒6²+8²=GC²
⇒36+64=GC²
⇒GC²=100=10²
⇒GC=10(cm)
Mà GC=2GI
⇒GI=GC2GC2 =102102=5(cm)
Vậy độ dài cạnh GI là 5cm
d)Ta có:
Theo b) GI=GK
⇒ΔIGK là tam giác cân tại G
{GC=2GIGB=2GK{GC=2GIGB=2GK
Mà GI=GK
⇒GC=GB
⇒ΔGBC là tam giác cân tại G
Ta có:
∠KIG=∠IKG=180∗−∠IGK2180∗−∠IGK2
∠GBC=∠GCB=180∗−∠BGC2180∗−∠BGC2
Mà ∠IGK=∠BGC(đối đỉnh)
⇒∠KIG=∠GCB
Mà 2 góc ở vị trí so le trong
⇒IK=BC

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

Áp dụng định lý \(Pi-ta -go \) và tam giác vuông \(ABC\) ta có :
\(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(=\sqrt{20^2+25^2}=5\sqrt{41}\) \(\left(cm\right)\)
Chu vi \(\Delta ABC\) là :\(AB+AC+BC=20+25+5\sqrt{41}=45+5\sqrt{41}\left(cm\right)\)

Diện tích tam giác ABC là:
6.8:2=24 (cm2)
Áp dụng định lí Py-ta-go cho tam giác ABC, ta có:
AB2+AC2=BC2
=>62+82=BC2=>36+64=BC2=>BC=10 (cm)
Đường cao AH dài là:
24.2:10=4,8 (cm)
Áp dụng định lí Py-ta-go cho tam giác ABH, ta có:
AH2+BH2=AB2
=>4,82+BH2=36
=>23,04+BH2=36
=>BH2=12,96=>BH=3,6 (cm)
Độ dài CH là:
10-3,6=6,4 (cm)
Đáp số: AH: 4,8 cm; BH: 3,6 cm; CH: 6,4 cm; BC: 10 cm
\(\text{Áp dụng định lý Pytago ta có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=6^2+8^2\)
\(\Rightarrow BC^2=100\)
\(\Rightarrow BC=10\left(\text{Vì BC}>0\right)\)
\(S_{\Delta ABC}\text{ là}:\)
\(\frac{6.8}{2}=24\)
\(\text{Vì AH là đường cao hạ từ đỉnh A và BC là đáy tương ứng với đường cao AH nên}\)
\(S_{\Delta ABC}=\frac{BC.AH}{2}=\frac{10.AH}{2}=24\)
\(\Rightarrow AH=24:5=4,8\)
\(\text{Áp dụng định lý Pytago ta có:}\)
\(AB^2=AH^2+BH^2\)
\(\Rightarrow6^2=4,8^2+BH^2\)
\(BH^2=12.96\)
\(BH=3,6\)
\(\text{CH thì tính tương tự như BH nha}\)