Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

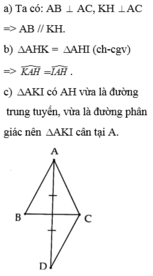
a) Ta có : AB vuông góc với AC
HK vuông góc với AC
AB // HK
b) ΔHAK=ΔHAI(c.g.c)(HA chung; HK = HI; AHKˆ=AHIˆ=900)
AK = AI Tam giác AKI cân tại A
c) Theo b : AIKˆ=AKIˆ
Mà BAKˆ=AKIˆ (cặp góc so le trong, AB // HK)
Từ 2 điều trên suy ra : BAKˆ=AIKˆ(=AKIˆ)
d) Tam giác IAK cân tại A có AH là đường cao ứng với đáy KI nên AH là đường phân giác xuất phát từ đỉnh A của tam giác AKI.
KACˆ=IACˆ
ΔAIC=ΔAKC(c.g.c) (AC chung; AK = AI (theo b); KACˆ=IACˆ(cmt))
1 đúng nhé
a) ta có :AB vuông góc AC
HK vuông góc AC
b) Xét tam giác AKH và tam giác AHI
AH là cạnh chung
H1 = H2
IH=HK (gt)
suy ra 2 tam giác trên bằng nhau
suy ra KA=AI
K^=I^
Vì KA=AI mà K = I nên tam giác KAI LÀ tam giác cân . Cân tại A

a) Ta có: AB⊥AC(ΔABC vuông tại A)
HK⊥AC(Gt)
Do đó: AB//HK(Định lí 1 từ vuông góc tới song song)
b) Xét ΔAKH vuông tại H và ΔAIH vuông tại H có
KH=IH(gt)
AH chung
Do đó: ΔAKH=ΔAIH(hai cạnh góc vuông)
Suy ra: AK=AI(hai cạnh tương ứng)
Xét ΔAKI có AK=AI(cmt)
nên ΔAKI cân tại A(Định nghĩa tam giác cân)
a) sử dụng tc: Từ vuông góc đến //
b)tam giác KHA= tam giác IHA(c.g.c)
=> AK=AI
=> góc AKI=góc AIK
vì AK=AI=> tam giác AKI cân
c) vì AB//HK=> góc BAK=góc AKI(so le trong)
góc BAK=góc AKI
mà góc AKI=góc AIK(cmt)
d) vì HC vuông góc với KI, KH=HI( GT) =>HC là trung trực=> KC=CI( t/c đường trung trực
tam giác AKC = tam giác AIC(c.c.c)

A B C H K I
mk vẽ ko có kí hiệu bn thông cảm
a) dễ thấy AB // HK ( vì cùng vuông góc với AC)
b) Vì \(AC\perp KI\)tại H và \(HK=HI\)nên AC là đường trung trực của KI
hay AH là đường trung trực của HI hay tam giác AKI cân tại A
c) Vì tam giác AKI cân tại A nên \(\widehat{AKI}=\widehat{AIK}\)
Mà \(\widehat{BAK}=\widehat{AKI}\)(2 góc so le trong)
=> \(\widehat{AIK}=\widehat{BAK}\)

A B C K H I
a,áp dụng định lý py-ta-go vào tam giác vuông ABC ta có
\(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
\(25=BC^2\)
\(\Rightarrow BC=5cm\)
b, Ta có :
\(\hept{\begin{cases}HK\perp AC\left(gt\right)\\AB\perp AC\left(\Delta ABC\perp A\right)\end{cases}}\)
\(\Rightarrow HK//AB\left(\perp AC\right)\)
c, Xét tam giác vuông AKH và tam giác vuông AIH có:
AH : cạnh chung
HI=HK(GT)
=> tam giác vuông AKH = tam giác vuông AIH ( 2 cạnh góc vuông )
=> AK = AI ( 2 cạnh tương ứng )
=> tam giác AKI cân tại A(AK = AI : 2 CẠNH BÊN)
d, ta có tam giác AKI cân tại A( cmt )
\(\Rightarrow\widehat{AIK}=\widehat{AKI}\)( 2 góc ở đáy) (1)
lại có HK // AB ( cmt)
=>\(\widehat{BAK}=\widehat{AKI}\)( 2 góc slt) (2)
từ (1) và (2) =>\(\widehat{AIK}=\widehat{BAK}\left(=\widehat{AKI}\right)\)
e, ta có tam giác vuông AKH = tam giác vuông AIH (cmt)
\(\Rightarrow\widehat{KAH}=\widehat{IAH}\)( 2 Góc tương ứng)
xét tam giác AIC và tam giác AKC có :
AK=AI(GT)
AC: cạnh chung
\(\widehat{KAH}=\widehat{IAH}\)(CMT)
=> tam giác AIC = tam giác AKC (C-G-C)
mk giải bài ktra cho các bn lớp 7a nè ko bt z đây mà chép
Câu 5 (bài cuối cùng ý)

A B C K H I
a/ Ta có
\(AB\perp AC\left(gt\right)\)
\(HK\perp AC\left(gt\right)\)
=> AB//HK (cùng vuông góc với AC)
b/ Xét tg AKI có
\(AH\perp HI\) => AH là đường cao của tg AKI
HK=HI (gt) => AH là trung tuyến của tg AKI
=> tg AKI cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
c/ Ta có
tg AKI cân tại A \(\Rightarrow\widehat{AIK}=\widehat{AKI}\) (góc ở đáy tg cân)
AB//HK (cmt) \(\Rightarrow\widehat{BAK}=\widehat{AKI}\) (góc so le trong)
\(\Rightarrow\widehat{BAK}=\widehat{AIK}\) (cùng bằng góc \(\widehat{AKI}\) )
d/ Xét tg CKI có
\(CH\perp KI\) => CH là đường cao của tg CKI
HK=HI => CH là trung tuyến của tg CKI
=> tg CKI cân tại C (Tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
Xét tg AIC và tg AKC có
tg AKI cân tại A (cmt) => AI=AK
tg CKI cân tại C (cmt) => CI=CK
AC chung
=> tg AIC = tg AKC (c.c.c)

B A C H E I D K
\(a)\)Xét \(\Delta ABH\) và \(\Delta KIH\) có:
\(HA=HK\left(gt\right)\)
\(\widehat{BHA}=\widehat{KHI}\left(đ^2\right)\)
\(HB=HI\left(gt\right)\)
\(\Rightarrow\Delta AHB=\Delta KIH\left(c.g.c\right)\)
\(b)\widehat{BAH}=\widehat{HKI}\left(\Delta AHB=\Delta KIH\right)\)
Mà hai góc ở vị trí so le trong
\(\Rightarrow AB//KI\)
\(c)AB\perp AC\)
\(AB//KI\)
\(\Rightarrow KI\perp AC\)
\(\Rightarrow IE\perp AC\)
\(\Rightarrow IK\equiv IE\)
\(\Rightarrow K,I,E\) thẳng hàng
\(d)\)Sai đề