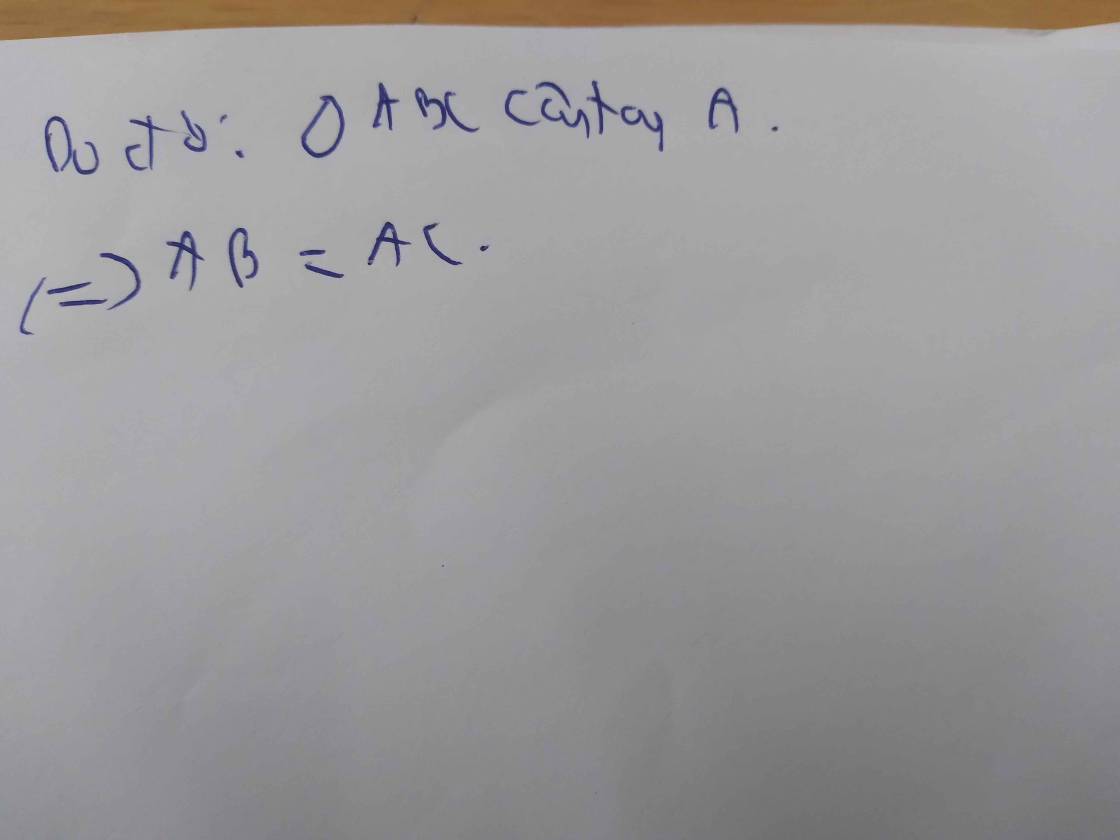Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
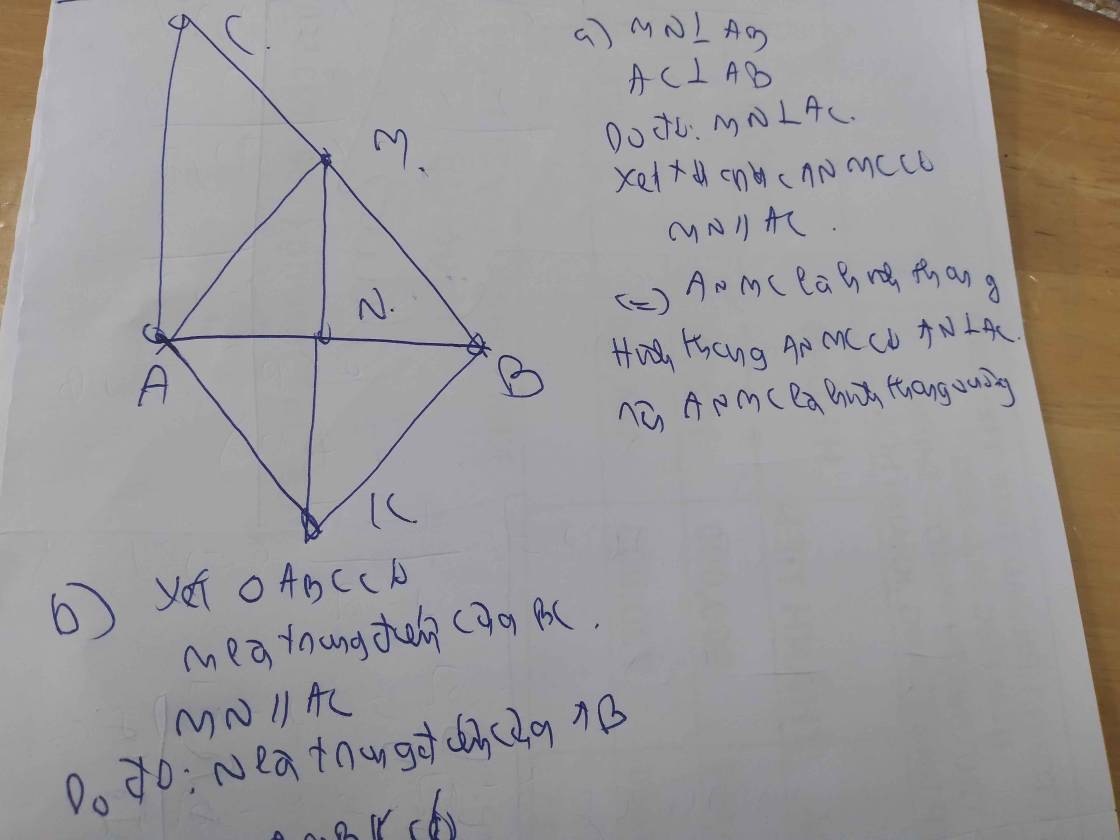
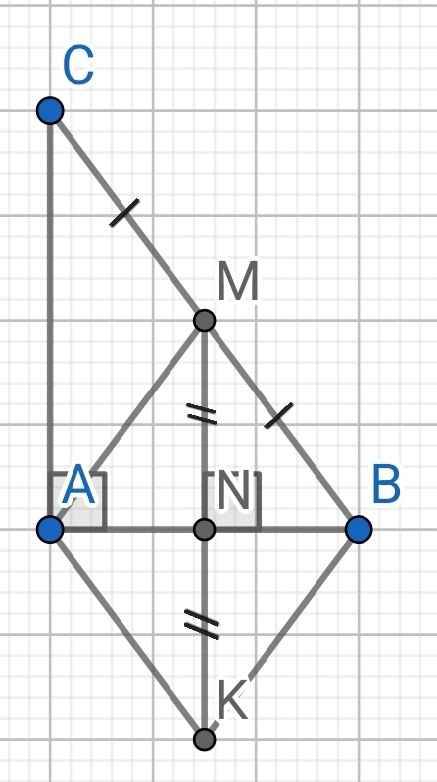a) Do MN ⊥ AB (gt)
AC AB (do ∆ABC vuông tại A)
⇒ MN // AC
Tứ giác ANMC có:
MN // AC (cmt)
⇒ ANMC là hình thang
Mà ∠CAN = 90⁰
⇒ ANMC là hình thang vuông
b) ∆ABC có:
MN // AC (cmt)
M là trung điểm của BC
⇒ N là trung điểm của AB
Do MN ⊥ AB (gt)
⇒ MK ⊥ AB
Tứ giác AKBM có:
N là trung điểm của AB (cmt)
N là trung điểm của MK (gt)
⇒ AKBM là hình bình hành
Mà MK ⊥ AB (cmt)
⇒ AKBM là hình thoi
c) Để AKBM là hình vuông thì
AM ⊥ MB
⇒ AM ⊥ BC
⇒ AM là đường cao của ∆ABC
Mà AM là đường trung tuyến của ∆ABC (do M là trung điểm của BC)
⇒ ∆ABC có AM vừa là đường cao, vừa là đường trung tuyến
⇒ ∆ABC cân tại A
Mà ∆ABC vuông tại A (gt)
⇒ ∆ABC vuông cân tại A
Vậy để AKBM là hình vuông thì ∆ABC vuông cân tại A
a) Tam giác ABC cân tại A có AM là đường trung tuyến
=> AM cũng là đường cao
=> AM⊥BC
Tứ giác AMCK có : I là trung điểm của đường chéo MK
I là trung điểm của đường chéo AC
=> AMCK là hình bình hành
mà góc AMC bằng 90 độ
=> AMCK là hình chữ nhật
b) Ta có: AK =MC ( 2 cạnh đối trong hình chữ nhật)
mà MC=MB ( M là trung điểm của BC)
=> AK=MB
Ta có: AK//MC( 2 cạnh đối trong hình chữ nhật)
mà MC và MB là 2 tia đối
=> AK//MB
Tứ giác AKBM có: AK=MB
AK//MB
=> AKBM là hình bình hành
c) Tứ giác ABEC có: M là trung điểm của đường chéo AE
M là trung điểm của đường chéo BC
=> ABEC là hình bình hành
mà AE⊥BC( cmt)
=> ABEC là hình thoi
Hình bạn có thể tự vẽ nha
a) Tứ giác AMCK là hình gì?Vì sao?
M,K đối xứng nhau qua I
=> I là trung điểm của MK (1)
I là trung điểm của AC (gt)(2)
(1)(2)=> AMCK là hình bình hành (3)
Tam giác ABC cân tại A có: AM là trung tuyến (gt)
=> AM vừa là trung tuyến vừa là đường cao (t/c)
=>AM vuông góc với BC
=> Góc BMC=90(4)
(3)(4)=> AMCK là hình chữ nhật(dhnb)
b) C/m ABEC là hình thoi:
AM=ME(gt)(5)
M nằm giữa A và E(6)
(5)(6)=>M là trung điểm AE(7)
M là trung điểm BC(8)
(7)(8)=> ABEC là hình bình hành(9)
AM vuông góc với BC,M thuộc AE=>AE vuông góc với BC(10)
(9)(10)=> ABEC là hình thoi (dhnb)
a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành
a: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
góc AMC=90 độ
=>AMCK là hình chữ nhật
b: Xet tứ giác ABMK có
AK//MB
AK=MB
=>ABMK là hình bình hành
c; Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
AB=AC
=>ABEC là hình thoi