Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAC có BD/BA=BM/BC
nên MD//AC và MD=1/2AC
=>ME//AC và ME=AC
=>AEMC là hình bình hành
b: Xét tứ giác ABFC có
M là trung điểm chung của AF và BC
góc BAC=90 độ
Do đó: ABFC là hình chữ nhật
c: AC=căn(5^2-3^2)=4cm
S=3*4=12cm2

a: Xét tứ giác AEMC có
ME//AC
ME=AC
Do đó: AEMC là hình bình hành

a: Xét ΔBAC có
M là trung điểm của BC
D là trung điểm của AB
Do đó: MD là đường trung bình của ΔBAC
Suy ra: MD//AC
hay ME\(\perp\)AB
mà ME cắt AB tại trung điểm của ME
nên E và M đối xứng nhau qua AB
b: Xét tứ giác AEMC có
AC//ME
AC=ME
Do đó: AEMC là hình bình hành

a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trun điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC; DM = 1/2AC
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành)
c) Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành ( D/h 5 )
mà AB vuông góc EM
=> hbh AEBM là hình thoi ( D/h 3 )
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền)
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm)
Chu vi hình thoi AEBM:
2,5 . 4 =10 (cm)
e) Nếu AEBM là hình vuông
thì Â= Ê= góc B= góc M= 90 độ
=>AM vuông góc BC
=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông

a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trung điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC;
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành
Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành
mà AB vuông góc EM
=> AEBM là hình thoi
c, Ta có : AM = ( trung tuyến ứng với cạnh huyền)
=> AM = (cm)
Chu vi hình thoi AEBM:
2 . 4 =8 (cm)
d, Nếu AEBM là hình vuông
thì = góc B= góc M= 90 độ
<=> AM vuông góc BC
<=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
<=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông
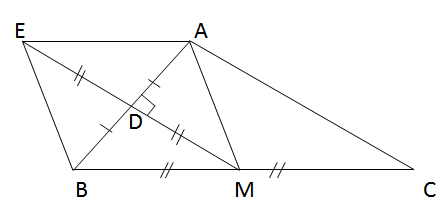
a) Ta có: MB = MC (giả thiết) ; DA = DB (Giả thiết)
⇒ DM là đường trung bình của Δ ABC
⇒ DM//AC
Mặt khác ABC vuông tại A
⇒ AC ⊥ AB ⇒ DM ⊥ AB
⇒ DE ⊥ AB (*)
E là điểm đối xứng với M qua D
⇒ DM = DE (**)
Từ (*) và (**) ta suy ra: Điểm E đối xứng với M qua AB
b) Ta có AB ⊥ EM và DE = DM, DA = DB
⇒ Tứ giác AEBM là hình thoi
⇒ AE//BM mà BM = MC ⇒ AE//MC và AE = MC
⇒ tứ giác AEMC là hình bình hàng
c) Ta có BC = 4 (cm) ⇒ BM = BC/2 = 2(cm)
Chu vi hình thoi ABEM là : P = 4BM = 8 (cm)
d) Hình thoi AEBM là hình vuông khi góc ∠AMB = 90 \(^0\)
⇒ AM ⊥ BC
Mặt khác: AM là trung tuyến của tam giác vuông ABC
Suy ra: Δ ABC vuông cân tại A
Điều kiện: Δ ABC vuông cân tại A

a) Xét tam giác ABC vuông tại A, có:
* AM là trung tuyến (gt)
=> AM = BM = MC (hệ quả)
=> tam giác BMA cân tại M
Mà MD là trung tuyến (D là trung điểm)
=> MD cũng là đường cao
Mà DM = DE (M đối xứng với E qua D)
=> E, M đối xứng nhau qua AB (do là đường trung trực) (đpcm)
b) Xét tam giác ABC, có:
* D là trung điểm AB(gt)
* M là trung điểm BC(AM là trung tuyến)
=> DM là đường trung bình
=> DM // AC (t/c)
=> DM = AC : 2 (t/c)
2DM = AC
Mà DM = DE (M đối xứng với E qua D)
=> EM = AC
Mà EM // AC (DM // AC, E thuộc DM)
=> AEMC là hình bình hành
c) Xét tam giác ABF, có:
* D, M lần lượt là trung điểm AB, AF
=> DM là đường trung bình
=> DM // BF
Mà DM // AC (cmt)
=> BF // AC
=> ABFC là hình thang
Ta có : BF // AC (cmt)
Mà AC vuông góc với AB (tam giác ABC vuông)
=> AC vuông góc với AB
Ta có ABFC là hình thang (cmt)
Mà góc B = góc A ( AC, AB cùng vuông góc với AB)
=> ABFC là hình thang cân (có 2 góc đáy bằng nhau)
Mà góc A = 90 độ (tam giác ABC vuông tại A)
=> ABFC là hình chữ nhật (đpcm)
a, Tam giác ABC vuông cân tại A nên AM vừa là trung tuyến cũng đồng thời là đường cao
+trung tuyến ứng với cạnh huyền = nửa cạnh huyền nên AM=MB
do đó tam giác AMB vuông cân tại M
suy ra điểm E đối xứng M qua D là trung điểm AB cũng đồng thời đối xứng M qua AB
b,Dễ có AEMC là hình bình hành . AEBM là hình vuông
c,
Chu vi AEBM bằng 2(AM+BM)=4AM=2BC=8 (cm)
d, AEBM là hình vuông khi tam giác ABC vuông
Bạn ơi bạn đọc lại đầu bài hộ Mk nhé!!.... Dù sao cũng thanks pn nhìu ạ!