Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nhé!!!
a) Vì tam giác ABC vuông tại nên theo ĐL Pytogo ta có:
BC2 = AB2 + AC2
=> 102 = 62 + AC2
=> AC2 = 102 - 62
=> AC2 = 64
=> AC = 8 (cm)
b) Vì BD là tia phân giác góc ABC nên
Góc ABD = góc DBH
Xét tam giác ABD và tam giác HBD có:
Góc A = góc BHD (=90 độ)
góc ABD = góc DBH (cmt)
cạnh BD chung
=> tam giác ABC = Tam giác HBD ( ch-gn)
=> AB = HB ( 2 cạnh tương ứng)
Tam giác ABH có AB = BH (cmt)
=> Tam giác ABH cân tại B
Mik k biết làm câu so sánh bạn thông cảm nhé!!!
Các bạn thấy đúng thì k sai thì thôi nha.

a.Xét tam giác ABD và HBD có:góc A = B=90 độ,BD cạnh chung,gócABD=HBD
Suy ra:tam giác ABD=HBD{cạnh huyền góc góc nhọn}
Suy ra:BA=BH
b.Suy ra: AD=DH
Suy ra: AD=DC

Bài 1 a, xét tam giác ABD và tam giác HBD có:
BD cạnh chung
\(\widehat{ABD}\)=\(\widehat{HBD}\)(gt)
\(\Rightarrow\)tam giác ABD = tam giác HBD( CH-GN)
\(\Rightarrow\)AB=HB
b,trên tia đối của tia DH lấy O sao cho HD=DO
xét tam giác ADO và tam giác CDH có:
DH=DO( theo trên)
\(\widehat{ADO}\)=\(\widehat{CDH}\)( Vì đối đỉnh)
\(\Rightarrow\)tam giác ADO=tam giác CDH( CH-GN)\(\Rightarrow\)AD=CD

A B C H D E 1 2 1 2 3 4
A) XÉT \(\Delta ABC\)VUÔNG TẠI A
\(BC^2=AB^2+AC^2\left(PYTAGO\right)\)
THAY \(BC^2=3^2+4^2\)
\(BC^2=9+16\)
\(BC^2=25\)
\(\Rightarrow BC=\sqrt{25}=5\left(cm\right)\)
XÉT \(\Delta ABC\) CÓ
\(BC>AC>AB\left(5>4>3\right)\)
\(\Rightarrow\widehat{A}>\widehat{B}>\widehat{C}\)QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
B) XÉT \(\Delta BAH\)VÀ\(\Delta BDH\)CÓ
BH LÀ CẠNH CHUNG
\(\widehat{H_2}=\widehat{H_1}=90^o\)
\(AH=DH\left(GT\right)\)
=>\(\Delta BAH\)=\(\Delta BDH\)(C-G-C)
=> AB = BD( ĐPCM)
C) XÉT \(\Delta BAH\)VÀ\(\Delta EDH\)CÓ
\(BH=EH\left(GT\right)\)
\(\widehat{H_2}=\widehat{H_4}\left(Đ^2\right)\)
\(AH=DH\left(GT\right)\)
=>\(\Delta BAH\)=\(\Delta EDH\)(C-G-C)
=>\(\widehat{A_1}=\widehat{D_2}\)HAI GÓC TƯƠNG ỨNG
HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG BẰNG NHAU
=> DE//AB
b)
Kẻ DH⊥BC(H∈BC)DH⊥BC(H∈BC)
△ABD và △HBD có:
ˆBAD=ˆBHD=90oBD:cạnh chungˆABD=ˆHBDBAD^=BHD^=90oBD:cạnh chungABD^=HBD^
⇒△ABD = △HBD (cạnh huyền - góc nhọn)⇒AD=HD⇒△ABD = △HBD (cạnh huyền - góc nhọn)⇒AD=HD
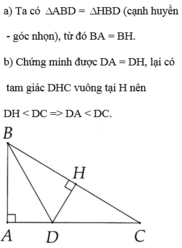
Mà △HCD vuông tại H nên DC > DH (cạnh huyền lớn hơn cạnh góc vuông)
Từ đó suy ra DC > AD
Bạn tham khảo nhé!