Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề:
Cho hình thang ABCD ( AB // CD ), AC cắt BD tại O. Đường thẳng // AB cắt các cạnh bên AD, BC và các đường chéo BD, AC theo thứ tự M, Q, N, P. Cm: MN = PQ.
Bài Làm: 
Chúc pạn thân hok tốt nhé!!!
A B C D O M N P Q
Xét \(\Delta ADB,\Delta ACB\) có :
\(MQ//AB\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{MN}{AB}=\dfrac{DM}{DA}\left(1\right)\\\dfrac{PQ}{AB}=\dfrac{CQ}{CB}\left(2\right)\end{matrix}\right.\text{(định lí Ta- lét)}\)
Xét hình thang ABCD có :
\(MQ//AB//CD\)
\(\dfrac{\Rightarrow DM}{DA}=\dfrac{CQ}{CB}\left(3\right)\)
- Từ (1) , (2) và (3) ta có :
\(\dfrac{MN}{AB}=\dfrac{PQ}{AB}\Rightarrow MN=PQ\)
=> đpcm

Hình bạn tự vẽ nhé
Áp dụng định lý Pi-ta-go vào tam giác AMN vuông tại A ta được:
\(AM^2+AN^2=MN^2\)
\(400=MN^2\)
\(\Rightarrow MN=20\)
Xét tam giác AMN có BC//MN
\(\Rightarrow\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)( Hệ qua của định lý Ta-let)
\(\Rightarrow\frac{2}{3}=\frac{20}{BC}=\frac{12}{AC}\)
\(\Rightarrow\hept{\begin{cases}BC=30\left(cm\right)\\AC=18\left(cm\right)\end{cases}}\)
Ta có: AN+NC=AC ( h.vẽ)
\(\Rightarrow NC=6\)(cm)
Vậy ...

MN//BC nên \(\frac{MN}{BC}=\frac{AM}{AB}\Rightarrow MN=\frac{5}{15}.20=\frac{20}{3}\)
MN//BC nên \(\frac{MN}{BC}=\frac{AN}{AC}\Rightarrow AN=\frac{\frac{20}{3}}{20}.12=4\)
NP//AB nên \(\frac{AN}{AC}=\frac{BP}{BC}\Rightarrow BP=\) thế số vào
MN//CD nên \(\frac{AM}{AD}=\frac{BN}{BC}\).Lại có \(\frac{Am}{AD}=\frac{OM}{CD}\left(1\right),\frac{BN}{BC}=\frac{ON}{CD}\left(2\right)\)
nên (1)=(2) \(\frac{OM}{CD}=\frac{ON}{CD}\RightarrowĐPCM\)

\(\Delta ABC\) có \(MN//BC\) áp dụng định lý Ta-lét ta có:
\(\frac{AM}{AB}=\frac{AN}{AC}\)
hay \(\frac{16}{24}=\frac{12}{AC}=\frac{MN}{BC}\)
\(\Rightarrow\)\(AC=\frac{24.12}{16}=18\) cm
Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=24^2+18^2=900\)
\(\Leftrightarrow\)\(BC=\sqrt{900}=30\)cm
Áp dụng định lí Ta-lét ta có:
\(\frac{MN}{BC}=\frac{AN}{AC}=\frac{AM}{AB}\Leftrightarrow\frac{MN}{BC}=\frac{12}{AC}=\frac{16}{24}=\frac{2}{3}\)
\(\Rightarrow\frac{12}{AC}=\frac{2}{3}\Leftrightarrow2AC=36\Leftrightarrow AC=18\left(cm\right)\)
\(AC=AN+NC\Leftrightarrow18=12+NC\Rightarrow NC=6\left(cm\right)\)
\(\text{ }\text{Áp dụng định lí Py-ta-go vào tam giác vuông ABC ta có:}\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow24^2+18^2=BC^2\)
\(\Leftrightarrow BC^2=900\Rightarrow BC=30\left(cm\right)\)
Vậy....

Trong ΔABC, ta có: MN // BC (gt)
Suy ra: 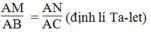
Suy ra: 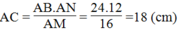
Vậy NC = AC – AN = 18 – 12 = 6(cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
M N 2 = A M 2 + A N 2 = 16 2 + 12 2 = 400
MN = 20cm
Trong ΔABC, ta có: MN // BC (gt)
Suy ra:![]()
Vậy: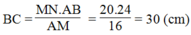

:V chụp xong không gửi được cái phần kia nên mình chép ra vậy hình bạn tự vẽ nhé v
a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Xét tam giác ABC có MN//BC (gt)
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{3}{4}=\frac{AN}{8}=\frac{MN}{10}\)
\(\Rightarrow\hept{\begin{cases}AN=6\left(cm\right)\\MN=7,5\left(cm\right)\end{cases}}\)
b)Vì MI//AC (gt)
\(\Rightarrow MI//AK\left(K\in AB\right)\)
Vì IK//AB(gt)
\(\Rightarrow IK//AM\left(M\in AB\right)\)
Ta có: \(\hept{\begin{cases}MI//AK\left(cmt\right)\\IK//AM\left(cmt\right)\end{cases}\Rightarrow MI=AK}\)( tc cặp đoạn chắn)
Ta có: AM+MB=AB
\(\Rightarrow MB=1,5\left(cm\right)\)
Xét tam giác ABC có MI//AB(gt)

Cho biểu thức B=\(\frac{2x+1}{x^2-1}\); A= \(\frac{3x+1}{x^2-1}\)--\(\frac{x}{x-1}\)+\(\frac{x-1}{x+1}\) (x khác +,- 1; x khác \(\frac{-1}{2}\))
a) Tính giá trị của B biết x=-2
b) Rút gọn A
c) Cho P=A:B Tìm x biết P=3
Cho biểu thức A=\(\left(\frac{2x-3}{x^2-9}-\frac{2}{x+3}\right):\frac{x}{x+3}\)(x khác +,- 3)
a) Rút gọn A
b) TÍnh giá trị của A khi x=\(-\frac{1}{2}\)
c) Tìm các giá trị nguyên của x để A nhận giá trị nguyên
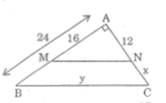
Bn tự vẽ hình nha!
Trong \(\Delta\)MAN vuông tại A có:
MN2 = AN2 + AM2
= 122 + 162
= 400
\(\Rightarrow\) MN = 20(cm)
Vì \(\Delta\)ABC có MN//AC (gt)
\(\Rightarrow\) \(\dfrac{MN}{BC}=\dfrac{AM}{AB}=\dfrac{AN}{AC}\)(hệ quả của định lí Ta- lét)
\(\Rightarrow\) \(\dfrac{20}{BC}=\dfrac{16}{24}=\dfrac{12}{AC}\)
\(\Rightarrow\) \(\dfrac{20}{BC}=\dfrac{12}{AC}=\dfrac{2}{3}\)
\(\Rightarrow\) BC = \(\dfrac{20.3}{2}\)= 30(cm)
\(\Rightarrow\) AC = \(\dfrac{12.3}{2}\)=18(cm)
\(\Rightarrow\) NC = AC - AN
= 18 - 12
= 60(cm)
Các pạn chỉ cần giúp mk Tính MN thui nha, những ý còn lại mk biết làm rùi!!!