Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
BC2=AB2+AC2BC2=AB2+AC2
⇔BC2=92+122=225⇔BC2=92+122=225
hay BC=15(cm)
Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên BDAB=CDACBDAB=CDAC(Tính chất tia phân giác của tam giác)
hay BD9=CD12BD9=CD12
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
BD9=CD12=BD+CD9+12=BC21=1521=57BD9=CD12=BD+CD9+12=BC21=1521=57
Do đó:
⎧⎪ ⎪⎨⎪ ⎪⎩BD9=57CD12=57⇔⎧⎪ ⎪⎨⎪ ⎪⎩BD=457cmCD=607cm{BD9=57CD12=57⇔{BD=457cmCD=607cm
Vậy: BD=457cm;CD=607cm

Sửa đề: Lấy E thuộc BC sao cho BE=BA
a: Chứng minh ΔBAD=ΔBED
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
=>ΔDEC vuông tại E
c: Sửa đề: Tia BA cắt ED tại F
Ta có: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>AF=EC

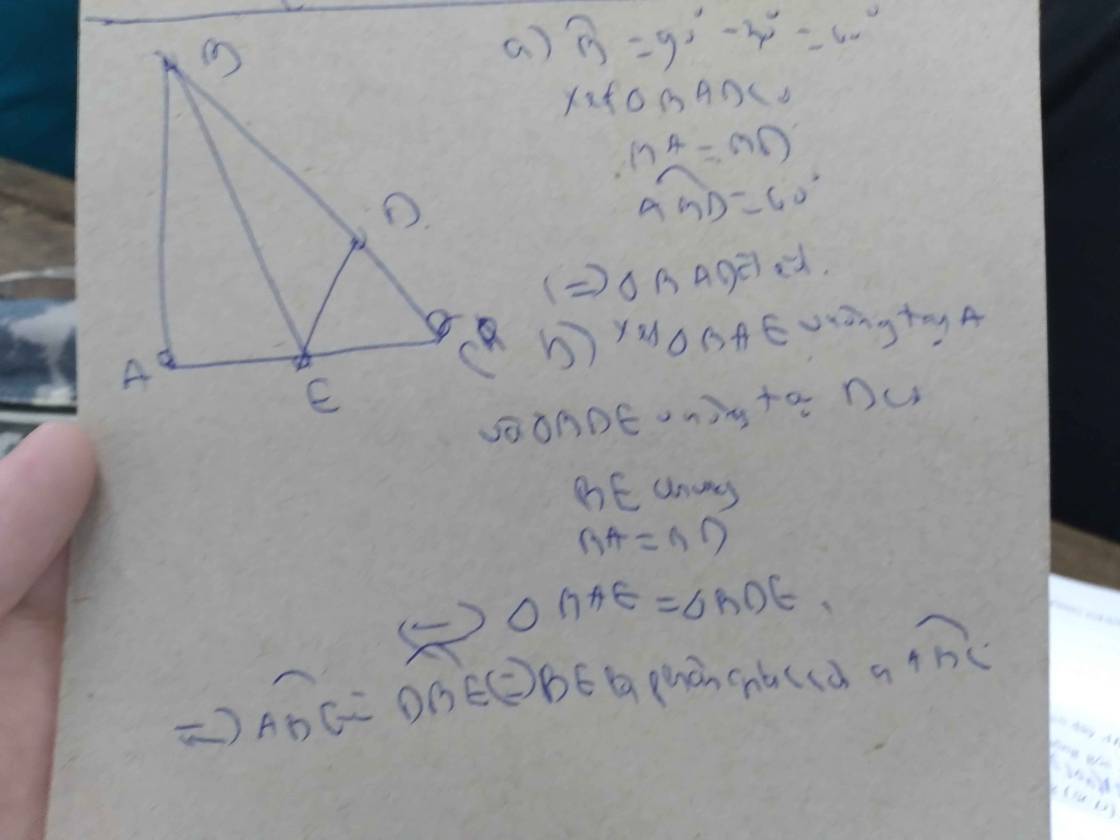
a) Xét ΔADB vuông tại A và ΔEDB vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔADB=ΔEDB(cạnh huyền-góc nhọn)
Suy ra: AD=ED(Hai cạnh tương ứng)
b) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(hai cạnh tương ứng)


Ta có: tam giác ABC vuông tại A
=> góc BAc=90độ hay góc BAD=90độ
Ta có: DE vuông góc với BC
=> góc BED =90độ
Xét tam giác BAD vuông tại A có:
góc ABD+ góc BDA =90độ (tổng 2 góc nhọn trong tam giác vuông)
=> Góc BDA=90độ -góc ABD
Xét tam giác BED vuông tại E có:
Góc DBE+góc BDE=90độ (tổng 2 góc nhọn trong tam giác vuông)
=> Góc BDE=90độ -góc DBE
Mà góc ABD=góc DBE (vì BD là tia p/g của góc ABC)
=> Góc BDA=góc BDE
Xét tam giác BDA và tam giác BDE ta có:
+>Góc ABD=góc EBD (vì BD là tia p/g của góc ABC)
+>Chung cạnh BD
+> Góc BDA=góc BDE (cmt)
=> tam giác BDA=tam giác BDE (g-c-g)
=>BA=BE (2 cạnh tương ứng)
=> ĐPCM
A B C E D
Xét t/g ABD và t/g EBD có:
góc BAD = góc BED = 90 độ
góc ABD = góc EBD (gt)
BD chung
=> t/g ABD = t/g EBD (ch - gn)
=> BA = BE