Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình ra hì. Mình vẽ ko được
Bài làm
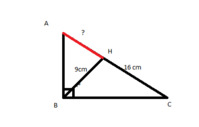
Tam giác AHB vuông tại H: AH^2+HB^2=AB^2
Tam giác AHC vuông tại H:AH^2+HC^2=AC^2
Tam giác ABC vuông tại A:BC^2=AB^2+AC^2
BC=HB+HC=9+16=25
BC^2=AH^2+HB^2+AH^2+HC^2=2AH^2+HB^2+HC^2=25^2=625
2HA^2+9^2+16^2=625
2HA^2+337=625
2HA^2=288
HA^2=144
HA=12

tự vẽ hình:::::
áp dụng định lí py-ta-go vào tam giác BHA vuông tại H ta được:
BH2+AH2=AB2(1)
áp dụng định lí py-ta-go vào tam giác AHC vuông tại H ta được:
HC2+AH2=AC2(2)
áp dụng định lí py-ta-go vào tam giác ABC vuông tại A ta được:
AB2+AC2=BC2(3)
Công hai vế (1);(2) kết hợp với (3) ta được:
HB2+HC2+AH2+AH2=AB2+AC2
92+162+2AH2=BC2
337+2AH2=(9+16)2
2AH2=625-337
2AH2=288
AH2=144
=>AH=√144=12(cm)
bạn ơi ko phải mk ko giúp mà về phần hình học mình dốt lắm

Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng hệ thức : AH^2 = HB . HC = 16 . 9
=> AH = 4 . 3 = 12 cm

Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm

cho tam giác ABC cân tại A, kẻ AH vuông góc BC ( H thuộc BC )
a) CHỨNG MINH GÓC BAH = GÓC CEB
b) CHO AH= 3 cm , BC= 8 cm . TÍNH ĐỘ DÀI AC
c) KẺ HE VUÔNG GÓC AB , HD VUÔNG GÓC AC , CHỨNG MINH AE=AD
d) CHỨNG MINH ED SONG SONG BC
trả lời :
A B C H 2cm 8cm
Xét \(\Delta\)ABC vuông tại A , có:
AH là đường cao (H\(\in\)BC)
Ta lại có: BC = HB + HC = 2 + 8 = 10 (cm) (1)
\(\Delta\)ABC vuông tại A
=> BC là cạnh huyền (2)
Từ (1) và (2) => AH = \(\frac{1}{2}\)BC = 4(cm)

`Answer:`
Có `BC=HB+HC=9+16=25cm`
Áp dụng định lý Pytago vào `\triangleABC` vuông tại `A=>BC^2=AB^2+AC^2(1)`
Áp dụng định lý Pytago vào `\triangleAHB` vuông tại `H=>AB^2=HB^2+AH^2(2)`
Áp dụng định lý Pytago vào `\triangleAHC` vuông tại `H=>AC^2=HC^2+AH^2(3)`
Từ `(1)(2)(3)=>AB^2+AC^2=HB^2+HC^2+AH^2+AH^2`
`=>BC^2=9^2+16^2+2AH^2`
`=>25^2=81+256+2AH^2`
`=>625 = 337 + 2AH²`
`=>2AH² = 625 - 337 = 288`
`=>AH^2=144`
`=>AH=\sqrt{144}=12cm`


A B C H 9cm 16cm AH=?
Chứng minh:
Xét \(\Delta ABC\) vuông tại A , có:
AH là đường cao (\(H\in BC\)).
Ta lại có: BC= BH + HC = 9 + 16 = 25 (cm). -> (1)
\(\Delta ABC\) vuông tại A => BC là cạnh huyền -> (2)
Từ (1) và (2) => \(AH=\frac{1}{2}BC=\frac{25}{2}=12,5\left(cm\right)\) (tính chất đường cao của tam giác vuông).
bài này chỉ có tui và nguyễn văn sử làm dc thui