Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

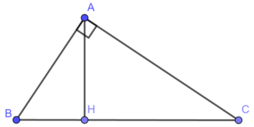
Đặt AB = c, AC = b, BC = a, AH = h là đường cao kẻ từ đỉnh A đến cạnh huyền BC
Vì tam giác ABC vuông tại A nên ta có: h = bc/a
*Khi quay tam giác vuông ABC một vòng quanh cạnh huyền BC thì cạnh AB và AC vạch nên hai hình nón chung đáy có bán kính đáy bằng đường cao AH và tổng chiều cao hai hình nón bằng cạnh huyền BC
Thể tích của hai hình nón:
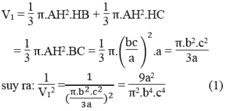
Khi quay tam giác vuông ABC một vòng quanh cạnh AB thì ta thu được hình nón có chiều cao AB = c, bán kính đáy AC = b
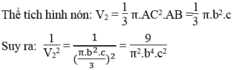
Khi quay tam giác vuông ABC một vòng quanh cạnh AC thì ta thu được hình nón có chiều cao AC=b,bán kính đáy AB=c
Thể tích hình nón:
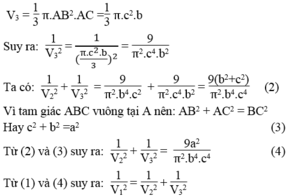

4. Dễ thấy \(\Delta AML\approx\Delta LKC\left(g-g\right)\)
\(\Rightarrow\frac{AL}{LC}=\sqrt{\frac{S_{\Delta AML}}{S_{\Delta LKC}}}=\sqrt{\frac{42.7283}{51.4231}}\approx0.9115461896\)
\(\Rightarrow\frac{AL}{AC}=\frac{0.9115461896}{0.9115461896+1}=0.476863282\)
Lại có \(\Delta AML\approx\Delta ABC\left(g-g\right)\)
\(\Rightarrow\frac{S_{AML}}{S_{ABC}}=\left(\frac{AL}{AC}\right)^2=0.476863282^2=0.2273985897\)
\(\Rightarrow S_{\Delta ABC}=\frac{S_{\Delta AML}}{0.2273985897}=\frac{42.7283}{0.2273985897}\approx187.9\left(cm^2\right)\)
1. Ta có \(\frac{BH}{CH}=\frac{\sqrt{7}}{\sqrt{5}}\Rightarrow BH=\frac{\sqrt{7}}{\sqrt{5}}CH\)
Mặt khác \(BC=\sqrt{11}\Rightarrow BH+CH=11\)
\(\Rightarrow\frac{\sqrt{7}}{\sqrt{5}}CH+CH=11\)
\(\Leftrightarrow CH=\frac{-55+11\sqrt{35}}{2}\) và \(BH=\frac{77-11\sqrt{35}}{2}\)
Có BH, CH và BC tính đc AB, AC \(\left(AB=\sqrt{BH.BC};AC=\sqrt{CH.BC}\right)\)
Từ đó tính đc chu vi tam giác ABC.
2. Để cj gửi hình qua gmail cho
3. Chỉ còn cách làm từng bước thôi e
\(B=31+\frac{27}{\frac{30127}{2008}}=31+\frac{54216}{30127}=32+\frac{24089}{30127}\)
Để viết liên phân số, ta bấm phím tìm thương và số dư:
(Mỗi số b1, b2, b3, ..., bn-1 chính là thương; số chia của phép chia trước là số bị chia của phép chia sau, còn số dư của phép chia trước là số chia của phép chia sau, nhớ nhá)
- B1: Tìm thương và số dư của 30127 cho 24089, thương là 1, dư 6038, viết \(B=32+\frac{1}{1+...}\)
- B2: Tìm thương và số dư của 24089 cho 6038, thương là 3, dư 5975, viết \(B=32+\frac{1}{1+\frac{1}{3+...}}\)
- B3: Tìm thương và số dư của 6038 cho 5975, thương là 1, dư 63, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+...}}}\)
- B4: Tìm thương và số dư của 5975 cho 63, thương là 94, dư 53, viết \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+...}}}}\)
...
Cứ làm như vậy, đến khi số dư là 1 thì dừng lại, phân số cuối cùng \(\frac{1}{b_n}\) thì bn chính là số chia cuối cùng, bn = 3
Kết quả: \(B=32+\frac{1}{1+\frac{1}{3+\frac{1}{1+\frac{1}{94+\frac{1}{1+\frac{1}{5+\frac{1}{3+\frac{1}{3}}}}}}}}\)

3)kẻ BD vuông góc voi71 BC, D thuộc AC
tam giác ABC cân tại A có AH là Đường cao
suy ra AH là trung tuyến
Suy ra BH=HC
(BD vuông góc BC
AH vuông góc BC
suy ra BD song song AH
suy ra BD/AH = BC/CH = 2
suyra 1/BD = 1/2AH suy ra 1BD^2 =1/4AH^2
tam giác BDC vuông tại B có BK là đường cao
suy ra 1/BK^2 =1/BD^2 +1/BC^2
suy ra 1/BK^2 =1/4AH^2 +1/BC^2
1) \(1+tan^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\) (đpcm).

Hướng dẫn làm bài:
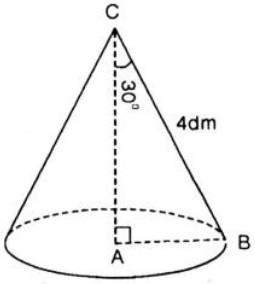
Trong tam giác vuông ABC, ta có:
AB=BC.sinC=BC.sin300=4.1/2=2(dm)
AC=BC.cosC=BC.cos300=4.√3/2=2√3(dm)
Ta có: Sxq = πRl = π. 2. 4 = 8 π (dm2)
V=1/3 π R2 h=1/3 π.22.2√3=8√3.π/3(dm3)

Bài 1:
a)
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2-AC^2}=\sqrt{10^2-8^2}=6\) (cm)
\(S_{ABC}=\frac{AC.CB}{2}=\frac{AB.CK}{2}\Rightarrow CK=\frac{AC.CB}{AB}=\frac{8.6}{10}=4,8\) (cm)
Áp dụng định lý Pitago:
\(BK=\sqrt{CB^2-CK^2}=\sqrt{6^2-4,8^2}=3,6\) (cm)
\(AK=BA-BK=10-3,6=6,4\) (cm)
b)
\(KH\perp BC, KI\perp AC\Rightarrow \widehat{KHC}=\widehat{KIC}=90^0=\widehat{HCI}\)
Tứ giác $KHCI$ có 3 góc vuông nên là hình chữ nhật.
c)
Xét tam giác $CHK$ và $CKB$ có:
Góc $C$ chung
\(\widehat{CHK}=\widehat{CKB}=90^0\)
\(\Rightarrow \triangle CHK\sim \triangle CKB(g.g)\)
\(\Rightarrow \frac{CH}{CK}=\frac{CK}{CB}\Rightarrow CH.CB=CK^2(1)\)
Hoàn toàn tương tự: \(\triangle CKI\sim \triangle CAK(g.g)\)
\(\Rightarrow \frac{CK}{CA}=\frac{CI}{CK}\Rightarrow CA.CI=CK^2(2)\)
Từ \((1);(2)\Rightarrow CH.CB=CA.CI\) (đpcm)
Bài 1:
d)
Vì \(HK\parallel AC\Rightarrow \frac{BH}{BK}=\frac{BC}{BA}\Rightarrow BH=\frac{BK.BC}{AB}\) (định lý Ta-let)
Tương tự: \(\frac{AI}{AK}=\frac{AC}{AB}\Rightarrow AI=\frac{AK.AC}{AB}\)
\(\Rightarrow \frac{AI}{BH}=\frac{AK}{BK}.\frac{AC}{BC}\)
Xét tam giác $BKC$ và $BCA$ có:
\(\left\{\begin{matrix} \text{góc B chung}\\ \widehat{BKC}=\widehat{BCA}=90^0\end{matrix}\right.\Rightarrow \triangle BKC\sim \triangle BCA(g.g)\)
\(\Rightarrow \frac{BK}{BC}=\frac{BC}{BA}\Rightarrow BK=\frac{BC^2}{BA}\) (cái này là công thức hệ thức lượng quen thuộc, mình chỉ chứng minh lại thôi nhé)
Tương tự: \(AK=\frac{AC^2}{AB}\)
\(\Rightarrow \frac{AK}{BK}=\frac{AC^2}{BC^2}(4)\)
Từ \((3);(4)\Rightarrow \frac{AI}{BH}=\frac{AC^2}{BC^2}.\frac{AC}{BC}=\left(\frac{AC}{BC}\right)^3\) (đpcm)
e)
Áp dụng những công thức thu từ phần d:
\(AB.BH.AI=AB.\frac{BK.BC}{BA}.\frac{AK.AC}{AB}=\frac{AK.BK.BC.AC}{AB}\)
Mà \(AK=\frac{AC^2}{AB}; BK=\frac{BC^2}{AB}\Rightarrow AB.BH.AI=\left(\frac{AC.BC}{AB}\right)^3\)
\(=\left(\frac{2S_{ABC}}{AB}\right)^3=CK^3\) (đpcm)
f)
Ta có: \(S_{KHI}=\frac{KH.KI}{2}=\frac{KM.HI}{2}\)
\(\Rightarrow KM=\frac{KH.KI}{HI}\Rightarrow KM^2=\frac{KH^2.KI^2}{HI^2}\)
\(\Rightarrow \frac{1}{KM^2}=\frac{HI^2}{KH^2.KI^2}=\frac{KH^2+KI^2}{KH^2.KI^2}=\frac{1}{KI^2}+\frac{1}{KH^2}\) (Pitago)
Mà theo phần b ta cm được $KHCI$ là hcn nên \(KI=CH; KH=CI\)
\(\Rightarrow \frac{1}{KM^2}=\frac{1}{CH^2}+\frac{1}{CI^2}\) (đpcm)

gọi D là tiếp điểm của đường tròn (K) trên BC . ta có DB = BE ; CD = CF (tính chất 2 tiếp tuyến cắt nhau)
\(\Rightarrow\) AE = AB + BE = c + BD
AF = AC + CF = b + CD
\(\Rightarrow\) AE + AF = b + c + (BD + CD)
= a + b + c
ta lại có AE = AF (tính chất 2 tiếp tuyến cắt nhau)
\(\Rightarrow\) AE = AF = \(\dfrac{a+b+c}{2}\) (đpcm)
b) BE = AE - AB = \(\dfrac{a+b+c}{2}\) - c = \(\dfrac{a+b-c}{2}\) (đpcm)
c) CF = AF - AC = \(\dfrac{a+b+c}{2}\) -b = \(\dfrac{a+c-b}{2}\) (đpcm)

Giải:
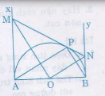
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3





