Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

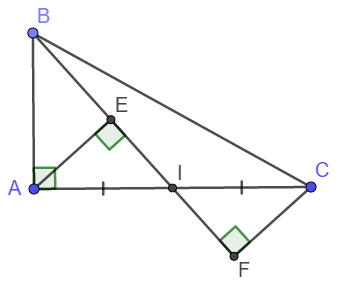
+) Xét tam giác vuông AEI và tam giác vuông CFI có:
AI = CI (gt)
\(\widehat{AIE}=\widehat{CIF}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AEI=\Delta CFI\) (Cạnh huyền - góc nhọn)
+) Theo quan hệ giữa đường xiên và đường vuông góc ta có:
\(AI>EI;IC>IF\Rightarrow AC>EF\) (đpcm)

B A C E F D
a.Xét \(\Delta ABD\) và \(\Delta EBD\) có:
\(\widehat{ABD}=\widehat{EBD}\) ( giả thiết)
BD - cạnh chung
\(\widehat{BAD}=\widehat{BED}\) ( = 90 do)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.h-g.n\right)\)
\(\Rightarrow AB=EB\) ( 2 cạnh tương ứng)
b.Xét \(\Delta ADF\) và \(\Delta EDC\) có:
\(\widehat{ADF}=\widehat{EDC}\) ( đối đỉnh)
AD = ED ( vi \(\Delta ABD=\Delta EBD\) )
\(\widehat{DAF}=\widehat{DEC}\) ( = 90 do)
\(\Rightarrow\Delta ADF=\Delta EDC\left(g.c.g\right)\)
=> DF = DC ( 2 cạnh tương ứng)
=> \(\Delta FDC\) cân tại D
c.Ta có:AB = EB (cm a)
=> \(\Delta ABE\) cân tại B
Mà BD là đường phân giác \(\widehat{ABE}\)
=> BD là đường trung trực của \(\Delta ABE\)
=> \(BD\perp AE\) (1)
Lại có: \(\Delta ADF=\Delta EDC\) ( cm b )
=>AF = EC ( 2 cạnh tương ứng)
Mà AB = BE => AB+AF=BE+EC
=> BF = BC. => \(\Delta BFC\) cân tại B
Mà BD là đường phân giác \(\widehat{ABC}\) hay \(\widehat{FBC}\)
=> BD là đường trung trực của \(\Delta FBC\)
=> \(BD\perp FC\) (2)
Từ (1),(2) => AE// FC ( dpcm)

a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABC}\), H∈BC)
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)
b) Ta có: ΔABC vuông tại A(gt)
⇒\(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Rightarrow\widehat{ACB}=90^0-\widehat{ABC}=90^0-60^0=30^0\)
Ta có: BE là tia phân giác của \(\widehat{ABC}\)(gt)
\(\Rightarrow\widehat{ABE}=\widehat{CBE}=\frac{\widehat{ABC}}{2}=\frac{60^0}{2}=30^0\)
Xét ΔEBC có \(\widehat{ECB}=\widehat{EBC}\left(=30^0\right)\)
nên ΔEBC cân tại E(định lí đảo của tam giác cân)
⇒EB=EC
Xét ΔEBH vuông tại H và ΔECH vuông tại H có
EB=EC(cmt)
EH chung
Do đó: ΔEBH=ΔECH(cạnh huyền-cạnh góc vuông)
⇒HB=HC(hai cạnh tương ứng)
c) Ta có: \(\widehat{BEC}\) là góc ngoài tại đỉnh E của ΔABE(EA và EC là hai tia đối nhau)
nên \(\widehat{BEC}=\widehat{BAE}+\widehat{ABE}\)(định lí góc ngoài của tam giác)
\(\Rightarrow\widehat{BEC}=90^0+30^0=120^0\)
Ta có: ΔEBH=ΔECH(cmt)
⇒\(\widehat{BEH}=\widehat{CEH}\)(hai góc tương ứng)
mà \(\widehat{BEH}+\widehat{CEH}=\widehat{BEC}\)(tia EH nằm giữa hai tia EB,EC)
nên \(\widehat{BEH}=\widehat{CEH}=\frac{\widehat{BEC}}{2}=\frac{120^0}{2}=60^0\)
\(\Leftrightarrow\widehat{KEH}=60^0\)
Ta có: HK//BE(gt)
⇒\(\widehat{BEH}=\widehat{KHE}\)(hai góc so le trong)
mà \(\widehat{BEH}=60^0\)(cmt)
nên \(\widehat{KHE}=60^0\)
Xét ΔKHE có
\(\widehat{KEH}=60^0\)(cmt)
\(\widehat{KHE}=60^0\)(cmt)
Do đó: ΔKHE đều(dấu hiệu nhận biết tam giác đều)
d) Xét ΔAEI vuông tại A có EI là cạnh huyền(EI là cạnh đối diện với \(\widehat{EAI}=90^0\))
nên EI là cạnh lớn nhất trong ΔAEI(trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
hay EI>EA
mà EA=EH(ΔBAE=ΔBHE)
nên IE>EH(đpcm)
Hung nguyenMashiro ShiinaXuân SángNhã DoanhnAkai HarumagonhuminhNguyễn Thanh Hằngnguyen thi Nguyễn Huy TúvangMến Hoàng Anh ThưVũPhạm Nguyễn Tất ĐạtVõ Đông Anh TuấnHoàng Lê Bảo NgọcPhương Ansoyeon_Tiểubàng giảiAce Legona