

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



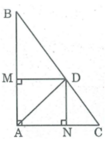
Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)
DM ⊥ AB (gt)
⇒ ∠ (AMD) = 90 0
DN ⊥ AC (gt) ⇒ ∠ (AND) = 90 0
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông

Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
mà AD là tia phân giác
nên AMDN là hình vuông

bạn tự vẽ hình nk.
cm: vì m, n lần lượt là chân đg vuông góc kẻ từ d dến ab,ac
=> tứ giác AMDN là hình chữ nhật (có 3 góc vuông) (dh nb hcn)
mặt #: ad là đg phân giác của góc a
=> hcn AMDN là hình vuông vì có có đường chéo là đường phân giác của góc a(dh nb hv)

Xét tứ giác AMDN, ta có: ∠∠(MAN) = 900900 (gt)
DM ⊥ AB (gt)
⇒∠∠(AMD) = 900900
DN ⊥ AC (gt) ⇒∠∠(AND) = 900900
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông

\(\text{GIẢI :}\)
A B C D N M
Chứng minh :
Ta có : M là chân đường vuông góc kẻ từ A đến AB \(\Rightarrow\text{ }\widehat{\text{M}}=90^{\text{o}}\).
N là chân đường vuông góc kẻ từ A đến AC \(\Rightarrow\text{ }\widehat{\text{N}}=90^{\text{o}}\)
Xét \(\diamond\text{AMDN}\) có \(\widehat{\text{A}}=\widehat{\text{M}}=\widehat{\text{N}}=90^{\text{o}}\)\(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình chữ nhật.
mà AD là đường phân giác của góc A \(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình vuông.

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: Ta có: ΔCEH vuông tại E
mà EK là đường trung tuyến
nên KE=KH
=>ΔKEH cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
mà \(\widehat{KHE}=\widehat{ABC}\)(hai góc so le trong, HE//AB)
nên \(\widehat{KEH}=\widehat{ABC}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{HAD}=\widehat{HED}\)
Ta có: \(\widehat{DEK}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{ABC}+\widehat{HAB}\)
\(=90^0\)
=>DE\(\perp\)EK