Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC\(\sim\)ΔABC(g-g)
d) Xét tứ giác AEHF có
\(\widehat{EAF}=90^0\)
\(\widehat{AEH}=90^0\)
\(\widehat{AFH}=90^0\)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
mk cần phần C và D bn có thể diễn giải chi tiết được không

a: Xet ΔABC vuông tại A và ΔHBA vuôngtại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: Xét ΔAEB và ΔIEC có
góc BAE=góc EIC
góc AEB=góc IEC
=>góc ABE=góc ICE=góc IBC
=>ΔIEC đồng dạng với ΔICB
=>IE/IC=IC/IB
=>IC^2=IE*IB
c: Xét ΔBNC có
BI vừa là phân giác, vừa là đường cao
=>ΔBNC cân tại B
=>I là trung điểm của NC
ΔNAC vuông tại A
mà I là trung điểm của NC
nên IA=IN=IC
=>IN^2=IE*IB
và IA=IM
nên IM^2=IE*IB
=>IM/IE=IB/IM
=>ΔIMB đồng dạng với ΔIEM
=>góc IMB=90 độ
=>ĐPCM

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
b) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)(Các cặp cạnh tuong ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)(đpcm)
b) Xét ΔCHA vuông tại H và ΔAHB vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔCHA\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{CA}{AB}=\dfrac{HA}{HB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AC}{HA}=\dfrac{AB}{BH}\)(1)
Xét ΔHBA có BI là đường phân giác ứng với cạnh AH(gt)
nên \(\dfrac{IA}{IH}=\dfrac{AB}{BH}\)(2)
Từ (1) và (2) suy ra \(\dfrac{IA}{IH}=\dfrac{AC}{HA}\)(3)
c) Xét ΔAHC có AK là đường phân giác ứng với cạnh CH(gt)
nên \(\dfrac{CK}{KH}=\dfrac{AC}{HA}\)(4)
Từ (3) và (4) suy ra \(\dfrac{CK}{KH}=\dfrac{AI}{IH}\)
hay KI//AC(Định lí Ta lét đảo)

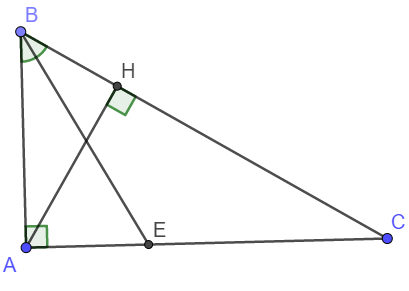
a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
Góc B chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right)\)
b)
Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
Góc C chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g-g\right)\)
c) Từ câu a và b ta có : \(\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB.HC=9.16=144\)
\(\Rightarrow HA=12\left(cm\right)\)
Khi đó áp dụng định lý Pi-ta-go ta có:
\(AB^2=BH^2+AH^2=9^2+12^2\Rightarrow AB=15\left(cm\right)\)
\(AC^2=CH^2+AH^2=16^2+12^2\Rightarrow AC=20\left(cm\right)\)
BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng tính chất tia phân giác trong tam giác ta có:
\(\frac{AE}{EC}=\frac{AB}{BC}=\frac{15}{25}=\frac{3}{5}\)
\(\Rightarrow AE=\frac{3}{8}\times20=7,5\left(cm\right)\)
\(\Rightarrow EC=20-7,5=12,5\left(cm\right)\)
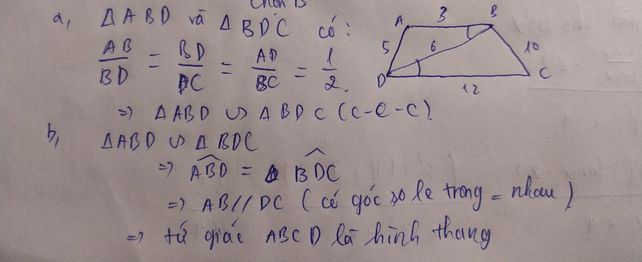 lời giải đây nhé e ❤️. tham khảo nhé!
lời giải đây nhé e ❤️. tham khảo nhé!