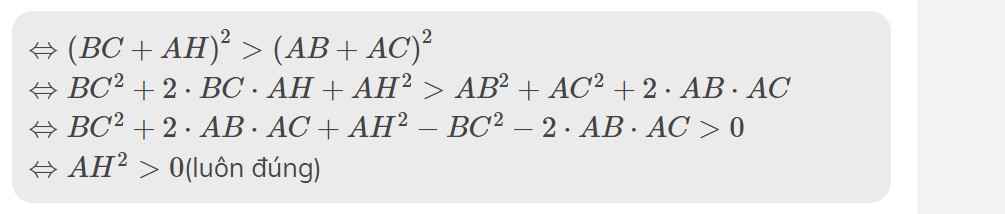HB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 6 2022
\(\Leftrightarrow\left(BC+AH\right)^2>\left(AB+AC\right)^2\)
\(\Leftrightarrow BC^2+2\cdot BC\cdot AH+AH^2>AB^2+AC^2+2\cdot AB\cdot AC\)
\(\Leftrightarrow BC^2+2\cdot AB\cdot AC+AH^2-BC^2-2\cdot AB\cdot AC>0\)
\(\Leftrightarrow AH^2>0\)(luôn đúng)
TA
25 tháng 3 2017
Tam giác ABC vuông tại A nên \(BC^2=AB^2+AC^2\)\(\Rightarrow\)\(BC^2-AB^2-AC^2=0\)
Mặt khác \(2AH.BC=2AB.AC\) (vì cùng bằng diện tích tam giác ABC).
BĐT cần CM tương đương với (AH + BC)2 > (AB + AC)2
hay \(AH^2+BC^2+2AH.BC>AB^2+AC^2+2AB.AC\)
\(\Leftrightarrow\)\(AH^2+\left(BC^2-AB^2-AC^2\right)+\left(2AH.BC-2AB.AC\right)>0\)
\(\Leftrightarrow\)\(AH^2>0\) (luôn đúng).
6 tháng 6 2016
Ta có: góc ABC = góc BAC + góc ACB (Tam giác abc vuông tại a)
=> BC = AB + AC (Quan hệ giữa góc và cạnh đối diện)
=> BC + AH > AB + AC
Hay AB + AC < BC + AH
HB
13 tháng 4 2018
a, Xét hai tam giác ABH và tam giác ADH có
BH=HD(giả thiết)
góc BHA=góc DHA(=90 độ)
AH chung
Suy ra ABH=ADH(dpcm)
b,c,d dài qúa mik ko ghi nổi bạn thông cảm nhé^^
6 tháng 5 2017
Câu a và b mình trả lời hộ bạn rùi. Bây giờ mình sẽ giải câu c.
A B C H N M K
Trên cạnh AB lấy điểm M sao cho BM=BH. Trên AH lấy điểm K sao cho HK=HN. Nối M với K và H.
Xét tam giác MNH: ^MNH=900 => ^NMH+^NHM=900 (1)
Lại có: ^KHM+^BHM=^KHB=900 . Mà BM=BH => Tam giác HBM cân tại B
=> ^BHM=^BMH => ^KHM+^BMH=900 (Thay vào biểu thức trên) hay ^KHM+^NMH=900 (2)
Từ (1) và (2) => ^NMH+^NHM=^KHM+^NMH=900 => ^NHM=^KHM=900-^NMH
Xét tam giác MNH và tam giác MKH có:
Cạnh MH chung
^NHM=^KHM => Tam giác MNH=Tam giác MKH (c.g.c)
HN=HK
=> MNH=^MKH (2 góc tương ứng) . Mà MNH=900 => ^MKH=900
MK vuông góc với AH => Tam giác MAK vuông tại K
=> AM là cạnh lớn nhất trong tam giác MAK (Quan hệ giữa góc và cạnh đối diện trong tam giác)
=> AM>AK => AB-BM>AH-HK (3) (Hệ thức cộng trừ đoạn thẳng)
Thay BM=BH và HK=HN theo cách vẽ vào (3), ta có:
AB-BH>AH-HN <=> AB>AH-HN+BH <=> HN+AB>AH+BH (Chuyển vế đổi dấu) (4)
Thay AH=HC vào (4), ta có: HN+AB>HC+HB => HN+AB>BC (đpcm)
--End--
\(\Delta\)