Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
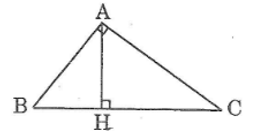
Cho tam giac ABC vuong tai A va đuong cao AH .Biet AB=15,HC=16.tinh chu vi va dien tich tam giac ABC

Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+16\right)=15^2=225\)
\(\Leftrightarrow BH^2+25HB-9HB-225=0\)
=>HB=9(cm)
BC=BH+CH=25(cm)
\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)
C=AB+BC+AC=15+20+25=60(cm)
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=15\cdot10=150\left(cm^2\right)\)

\(\Delta ABH\sim\Delta CAH\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{C_{ABC}}{C_{CAH}}=\dfrac{30}{40}=\dfrac{3}{4}\)
=> \(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}\)
\(\Rightarrow\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\\\)
=> \(\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(\Delta ABH\sim\Delta CBA\)
\(\Rightarrow\dfrac{C_{ABH}}{C_{ABC}}=\dfrac{AB}{BC}\)
=> Chu vi tam giác ABC là 30 . 5 : 3 = 50
Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có: