Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

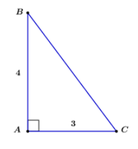
Tam giác ABC vuông tại A, áp dụng định lý Py-ta-go ta có:
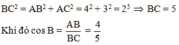
Đáp án cần chọn là: D

Theo pytago tính đc BC = 5cm.
Áp dụng công thức AB^2 = BH.BC từ đó ta tính đc BH

b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

mik ko bít
I don't now
................................
.............

ta có:cosB=\(\dfrac{AB}{BC}=\dfrac{5}{13}\)⇒BC=39
AC=\(\sqrt{BC^2-AB^2}=\sqrt{39^2-15^2}\)=36

\(AB=\dfrac{AC}{\tan B}=\dfrac{8}{\tan30^0}=\dfrac{8}{\dfrac{\sqrt{3}}{3}}=8\sqrt{3}\)

Hướng dẫn:
∆
ABC ∼
∆
HAC nên 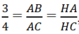
Suy ra HC = 4/3HA = 12. Chọn C.
\(BC=\sqrt{AC^{2}+AB^{2}}=\sqrt{3^{2}+4^{2}}=5\)
\(cosB=\dfrac{AB}{BC}=\dfrac{4}{5}=0,8\)