K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

10 tháng 1 2024
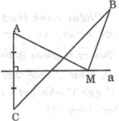
a: M nằm trên đường trung trực của AC nên MA=MC
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
TH1: M nằm giữa B và C
=>BM+CM=BC
=>MA+MB=BC=10cm
TH2: B,M,C không thẳng hàng
=>B,M,C tạo thành ΔBMC
Xét ΔMBC có MB+MC>BC
=>MB+MA>10
Do đó; MB+MA>=10
b: Vì \(MB+MA>=10\)
nên \(\left(MB+MA\right)_{min}=10\) khi MB+MC=10
=>MB+MC=BC
=>M nằm giữa B và C
=>M là giao điểm của xy với BC

CM
2 tháng 8 2017
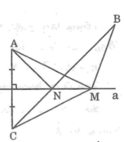
Theo chứng minh trên, khi M trùng với N thì MA + MB = BC bé nhất. Vậy khi M là giao điểm của BC với đường thẳng a thì MA + MB bé nhất.