Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

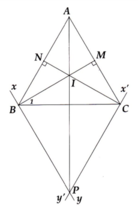
A B C N M x y
a, ^NAC + ^BAC + ^MAB = 180 (kb)
^BAC = 90
=> ^NAC + ^MAB = 90
^NAC + ^NCA = 90
=> ^NCA = ^MAB
xét tam giác CNA và tam giác AMB có : AB = AC do tam giác ABC vc (gt)
^CNA = ^AMB = 90
=> tam giác CNA = tam giác AMB (ch-gn)
b, tam giác CNA = tam giác AMB (câu a)
=> NA = BM (đn) và CN = AM (đn)
có : NA + MA = MN
=> BM + CN = MN
c, NC = AM (câu b) => NC^2 = AM^2
xét tam giác MB vuông tại M => BM^2 + AM^2 = AB^2 (pytago)
=> BM^2 + NC^2 = AB^2
mà AB không phụ thuộc vào xy
=> BM^2 + CN^2 không phụ thuộc vào xy

A B C x y M N
a) Ta có: \(\widehat{BAM}+90^0+\widehat{CAN}=180^o\)
\(\Rightarrow\widehat{BAM}+\widehat{CAN}=90^0\) (1)
Lại có: \(\widehat{ACN}+\widehat{CAN}=90^0\)(tính chất của tam giác vuông) (2)
Từ (1) và (2), suy ra: \(\widehat{BAM}=\widehat{ACN}\)
Xét \(\Delta BAM\perp M\) và \(\Delta CAN\perp N\), ta có:
BA = AC (gt)
\(\widehat{BAM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta BMA=\Delta CNA\) (cạnh huyền - góc nhọn)
b) Vì \(\Delta BMA=\Delta CNA\) (theo câu a)
Nên BM = AN (2 cạnh tương ứng) (3)
và MA = NC ( 2 cạnh tương ứng) (4)
Ta có: MA + AN = MN (5)
Nên thay (3), (4) vào (5) ta được BM + CN = MN (đpcm)
Chúc you học tốt nhé!!!!~~~~![]()

Xét ΔABD và ΔCAE có:
Góc ADB=Góc CEA=90
AB=AC
GócABD=Góc CAE( cùng phụ góc BAD)
=>ΔABD=ΔCAE
b) Ta có ΔABD=ΔCAE
=> AD=CE và BD=AE
=>BD+CE=AE+AD=ED

Bạn có thể tham khảo tại đây: Chứng minh BM^2+CN^2 không phụ thuộc vào vị trí của xy biết tam giác ABC vuông cân tại A - Phạm Phú Lộc Nữ
Chúc bn học tốt!