Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)xét tứ giác ADME có
CÂB =AÊM=góc ADM=900
=>ADME là hcn
b)vì MA là đg trung tuyến nên MA=MC=MB
xét tam giác CMA có
CM=MA(cmt)
CÊM=AÊM=900
EM là cạnh chung
=>...(cạnh huyền-cạnh góc vuông)
=>CE=EA
mà EA=MD(EAMD là hcn) nên CE=MD (1)
ta có MA=MC(cmt)
mà MA=ED(EAMD là hcn)
=>MC=ED (2)
xét tứ giác CMDE có CE=MD,CM=ED( 1 và 2)
=>CMED là hbh
c)
xét tam giác MDB vuông tại D có DI là trung tuyến nên MI=IB=ID
xét tứ giác MKDI có
KM=KD(K là giao điểm hai dg chéo của hcn)
KM=MI(vì MA=MB mà K và I lần lượt là trung điểm của chúng)
MI=ID(cmt)
=>KMID là thoi
mà KI là đg chéo của góc I nên KI cũng là p/g của góc I
(ck hk tốt nhé)

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó:ADME là hình chữ nhật
Suy ra: DE=AM
b: Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
M là trung điểm của bC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
E là trung điểm của AC
M là trung điểm của BC
DO đó: EM là đường trung bình
=>EM//AB và EM=AB/2
=>EM//BD và EM=BD
hay BDEM là hình bình hành
c: Ta có: BDEM là hình bình hành
mà O là giao điểm của hai đường chéo
nên O là trung điểm chung của BE và DM
Xét ΔEBC có
O là trung điểm của EB
I là trung điểm của CE
Do đó: OI là đường trung bình
=>OI=BC/2
mà AM=BC/2
nên OI=AM
Xét tứ giác AOMI có MO//AI
nên AOMI là hình thang
mà OI=AM
nên AOMI là hình thang cân

1a/IM vuông góc AB=>AMI=90 do
IN vuông góc AC=>ANI=90 do
△ABC vuông tại A=>BAC=90 do
=>góc AMI= gocANI= gocBAC= 90 do => tứ giác AMIN là hình chữ nhật
1b/Có I dx vs D qua N => ID là đường trung trực của AC=>AI=AD; IC=ID(1)
Trong △ABC có AI là đường trung tuyến ứng với cạnh huyền BC =>AI=1/2BC hay AI=IC(2)
Từ (1) va (2) => AI=IC=CD=DA => Tu giac AICD la hthoi
2a/ Có M là TĐ AB và M là điểm đối xứng giữa E và H
=> AM=MB VA EM=MH hay AB giao voi EH tai TD M
=> Tg AEBH la hbh co AHB=90 do => Hbh AEBH la hcn
2b/Co AEBH la hcn=>EH=AB
+) Mà AB=AC=>EH=AC(1)
+) △ABC cân tại A có AH là đường cao đồng thời phân giác của góc BAC => góc BAH=góc HAC.
Co goc BAH=1/2 EAH ; góc AHE=1/2AHB
Ma goc EAH= goc AHB=>BAH=AHE hay goc HAC= goc AHE.
Mà 2 góc này ở vị trí SLT=> EH//AC(2)
Từ (1) va (2)=>tg AEHC la hbh

Lời giải
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???

a: Xét tứ giác ADCH có
M là trung điểm của AC
M là trung điểm của HD
Do đó: ADCH là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên ADCH là hình chữ nhật
b: Xét tứ giác ADHE có
HE//AD
HE=AD
Do đó:ADHE là hình bình hành

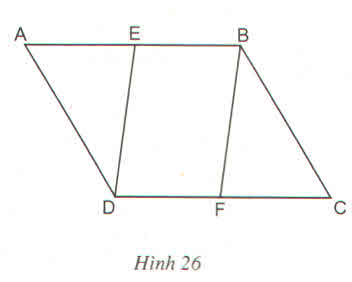
a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
b: ta có: DEBF là hình bình hành
nên Hai đường chéo DB và EF cắt nhau tại trung điểm của mỗi đường(1)
Ta có:ABCD là hình bình hành
nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,EF,AC đồng quy
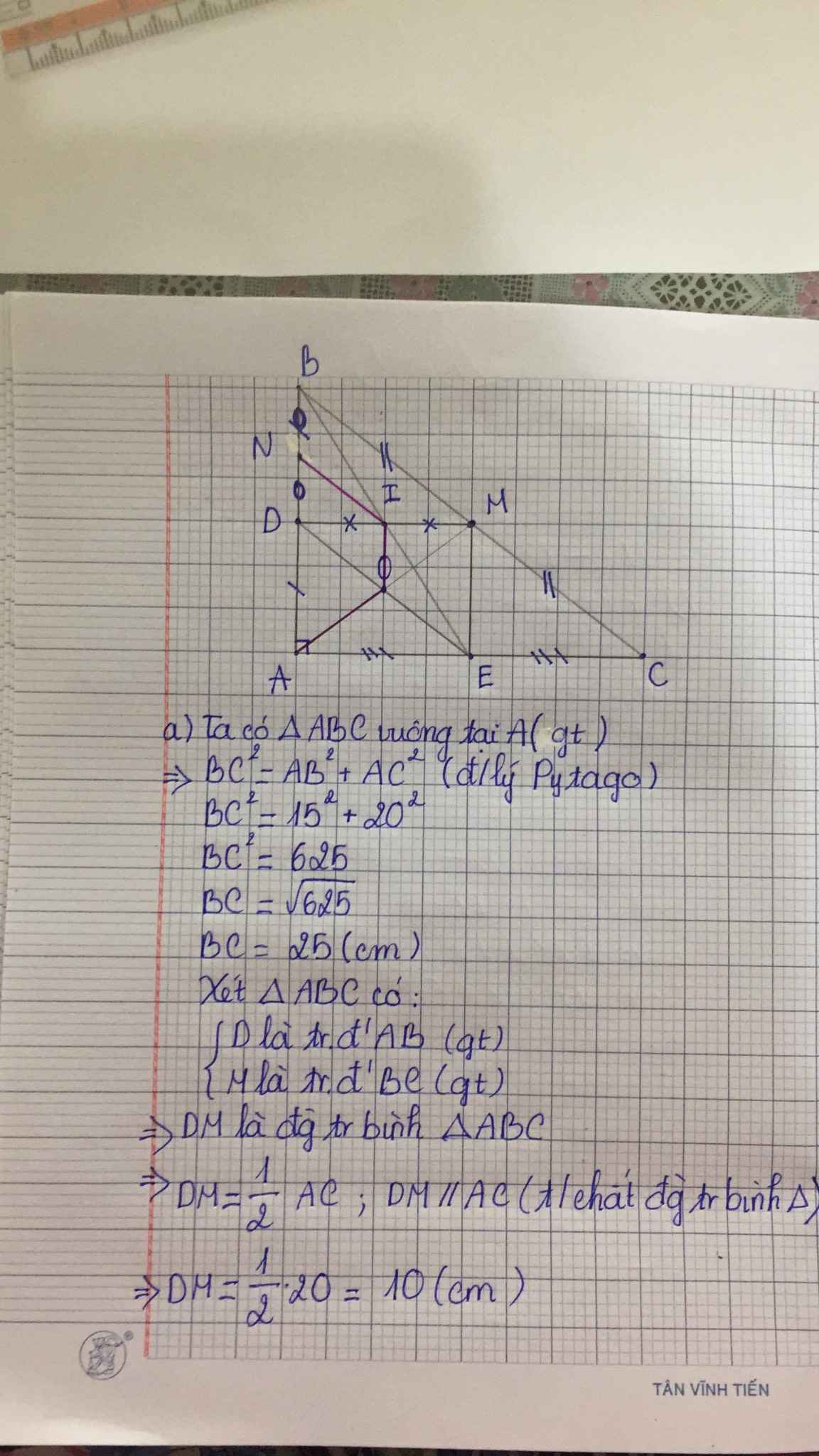





a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=25(cm)
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình của ΔABC
Suy ra: \(DM=\dfrac{AC}{2}=10\left(cm\right)\)