Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

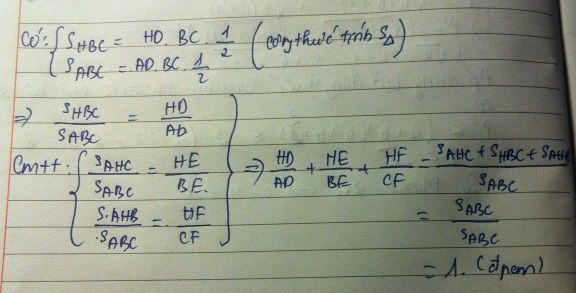
A B C D F E H Ta có : \(\dfrac{HD}{AD}=\dfrac{S_{HBC}}{S_{ABC}}\)( Do có chung đáy BC nên tỉ số hai đường cao bằng tỉ số hai diện tích) ( *)
Tương tự , ta có : \(\dfrac{HE}{BE}=\dfrac{S_{HAC}}{S_{ABC}}\) (**) Và \(\dfrac{HF}{CF}=\dfrac{S_{HAB}}{S_{ABC}}\)(***)
Từ ( *; **; ***) Ta có được :
\(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{HAC}+S_{HBC}+S_{HAB}}{S_{ABC}}=\dfrac{S_{ABC}}{S_{ABC}}=1\)

A B C D E F H
Ta có: \(\dfrac{AD.BC}{2}=S_{ABC}\Rightarrow AD=\dfrac{2S_{ABC}}{BC}\)
\(\Rightarrow\dfrac{HD}{AD}=\dfrac{HD.BC}{2S_{ABC}}\)
Tương tự: \(\dfrac{HE}{BE}=\dfrac{HE.AC}{2S_{ABC}};\dfrac{HF}{CF}=\dfrac{HF.AB}{2S_{ABC}}\)
\(\Rightarrow\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{BHC}+S_{AHC}+S_{AHC}}{S_{ABC}}=1\)


1. Vẽ hình và đặt tên:
2. Chứng minh các tam giác đồng dạng:
3. Tính diện tích:
4. Áp dụng bất đẳng thức Cauchy-Schwarz:
5. Chứng minh bất đẳng thức chính:
6. Kết luận:
nhìn câu trả lời kiệu @-@