Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình.
a, Sử dụng định lí pitago tính được \(BC=5cm\)
b, Dễ dàng chứng minh \(\Delta ABK=\Delta IBK\left(c.g.c\right)\)
=> \(\widehat{BIK}=\widehat{BAK}=90^o\)
=> \(KI\perp BC\)
c, Ta có: \(\hept{\begin{cases}AH\perp BC\\KI\perp BC\end{cases}}\)
=> AH // KI
=> \(\widehat{HAI}=\widehat{KIA}\) (1)
Mà AK = KI (do \(\Delta ABK=\Delta IBK\))
=> \(\Delta AKI\) cân tại K
=> \(\widehat{KAI}=\widehat{KIA}\) (2)
Từ (1) và (2) => \(\widehat{HAI}=\widehat{KAI}\)
=> AI là tia phân giác \(\widehat{HAC}\)
d, \(\Delta AEK\) có AI là phân giác => \(\Delta AEK\) cân tại A

Có gì khong hiểu hỏi lại cj nhé:
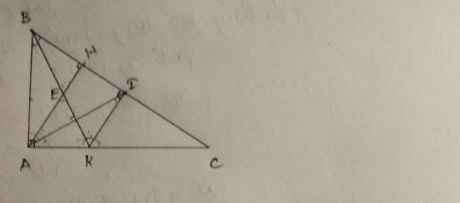
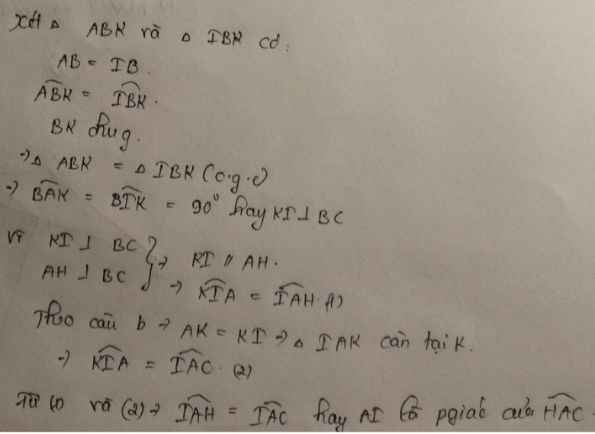
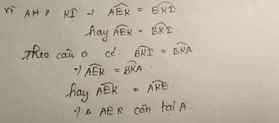
a, b ,c lần lượt từ trên xuống.

a: Xét ΔABK và ΔIBK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔABK=ΔIBK
Suy ra: \(\widehat{BAK}=\widehat{BIK}=90^0\)
hay KI⊥BC
b: Ta có: \(\widehat{HAI}+\widehat{BIA}=90^0\)
\(\widehat{CAI}+\widehat{BAI}=90^0\)
mà \(\widehat{BIA}=\widehat{BAI}\)
nên \(\widehat{HAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc HAC

a: Xét ΔABD và ΔIBD có
BA=BI
\(\widehat{ABD}=\widehat{IBD}\)
BD chung
Do đó: ΔABD=ΔIBD

bn tham khảo tại đây;
https://olm.vn/hoi-dap/detail/256733768368.html

a.Ta có:
⎧⎪⎨⎪⎩BA=BEˆABD=ˆDBEchungBD→ΔABD=ΔEBD(c.g.c){BA=BEABD^=DBE^chungBD→ΔABD=ΔEBD(c.g.c)
b.Từ câu a→ˆBED=ˆBAD=90o→BED^=BAD^=90o
→DE⊥BC→DE⊥BC
c.Ta có:
ˆBKD+ˆADK=ˆACB+ˆDEC=90oBKD^+ADK^=ACB^+DEC^=90o
→ˆBKD=ˆACB→BKD^=ACB^
→ΔBDK=ΔBDC(g.c.g)→ΔBDK=ΔBDC(g.c.g)
→BK=BC→BK=BC

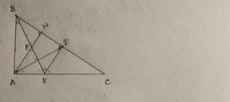
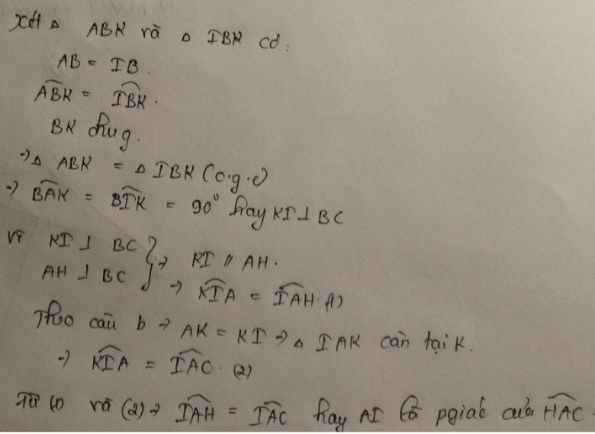

Hình bạn tự vẽ :
Xét \(\Delta ABK\)và \(\Delta IBK\)có :
\(BI=BA\left(gt\right)\)
\(\widehat{ABK}=\widehat{IBK}\left(gt\right)\)
\(BK\)chung
= > \(\Delta ABK=\Delta IBK\left(c.g.c\right)\)
= > \(\widehat{A}=\widehat{I}=90^0\)
hay \(KI\perp BC\)