Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo ạ!

O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD

\(y=3x+m\)(*)
1) a) Đồ thị hàm số (*) đi qua \(A\left(-1,3\right)\)nên \(3=3.\left(-1\right)+m\Leftrightarrow m=6\).
b) Đồ thị hàm số (*) đi qua \(B\left(-2,5\right)\)nên \(5=3.\left(-2\right)+m\Leftrightarrow m=11\).
2) Đồ thị hàm số (*) cắt trục hoành tại điểm có hoành độ \(3x+m=0\Leftrightarrow x=-\frac{m}{3}\)
Suy ra \(-\frac{m}{3}=-3\Leftrightarrow m=9\).
3) Đồ thị hàm số (*) cắt trục tung tại điểm có tung độ \(y=3.0+m=m\)
suy ra \(m=-5\).

a, Gọi I là trung điểm AB
Xét tam giác AEB vuông tại E, I là trung điểm
=> \(EI=AI=IB=\frac{AB}{2}\)(1)
Xét tam giác ADB vuông tại D, I là trung điểm
=> \(DI=AI=IB=\frac{AB}{2}\)(2)
Từ (1) ; (2) => A ; D ; B ; F cùng nằm trên đường tròn (I;AB/2)
b, Gọi O là trung điểm AC
Xét tam giác AFC vuông tại F, O là trung điểm
=> \(FO=AO=CO=\frac{AC}{2}\)(3)
Xét tam giác CDA vuông tại D, O là trung điểm
=> \(DO=AO=CO=\frac{AC}{2}\)(4)
Từ (3) ; (4) => A ; D ; C ; F cùng nằm trên đường tròn (O;AC/2)
c, Gọi T là trung điểm BC
Xét tam giác BFC vuông tại F, T là trung điểm
=> \(FT=BT=CT=\frac{BC}{2}\)(5)
Xét tam giác BEC vuông tại E, T là trung điểm
=> \(ET=BT=CT=\frac{BC}{2}\)(6)
Từ (5) ; (6) => B ; C ; E ; F cùng nằm trên đường tròn (T;BC/2)
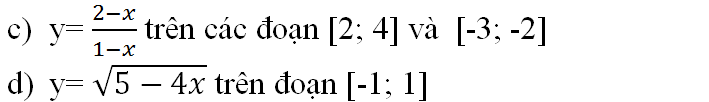

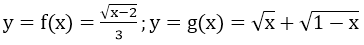
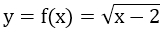 với x ≥ 2
với x ≥ 2

Ta có:
(sinC) ^ 2 + (cosC) ^ 2 = (AB / BC) ^ 2 + (AC / BC) ^ 2
=(AB ^ 2 + AC ^ 2) / BC ^ 2 = BC ^ 2 / BC ^ 2 = 1
(Vì ABC vuông tại A mà, nên theo pitago)
-->(cosC) ^ 2 = 1 - (sinC) ^ 2 = 1 - 0,8 ^ 2 = 0,36
--> cosC = 0,6 hoặc cosC = - 0,6 (loại vì C là 1 góc nhọn)
Vậy cosC = 0,6
tanC = 0,8 / 0,6 = 4 / 3, cotC = 0,6 / 0,8 = 0,75